Определение. Если 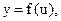 а
а 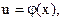 то
то 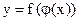 называется сложной функцией.
называется сложной функцией.
Замечание. Аргумент 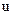 будем называть зависимым аргументом, а
будем называть зависимым аргументом, а 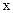 - независимым аргументом. Но в формуле
- независимым аргументом. Но в формуле 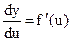 мы предполагаем, что производная определена, когда
мы предполагаем, что производная определена, когда 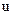 - независимый аргумент.
- независимый аргумент.
Теорема. Если существуют (конечные) производные 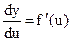 и
и 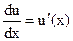 , то существует производная
, то существует производная 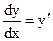 и
и 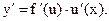
Пример 25.1. Если х независимый аргумент, то из §21 следует 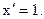 Аналогично
Аналогично 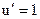 , если u является независимым аргументом. Формула
, если u является независимым аргументом. Формула 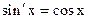 не всегда удобна, т.к. здесь нужно подразумевать, что х – независимый аргумент. Но если чуть поправить
не всегда удобна, т.к. здесь нужно подразумевать, что х – независимый аргумент. Но если чуть поправить 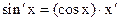 , то мы получим универсальную формулу. В литературе, как правило, она приводится в следующем виде
, то мы получим универсальную формулу. В литературе, как правило, она приводится в следующем виде 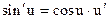 . Буквой х, как правило (но не всегда), обозначается независимый аргумент.
. Буквой х, как правило (но не всегда), обозначается независимый аргумент.
Пример 25.2. 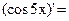 обозначим
обозначим 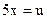 = =
= = 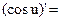
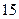 =
= 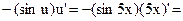 9 и 7=
9 и 7= 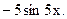
 2015-07-14
2015-07-14 226
226








