Геометрический смысл производной

Определение производной

Определение. Пусть 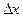- некоторая величина, которую назовем приращением аргумента. Тогда 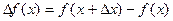назовем приращением функции.

Определение. Производной от функции 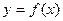в точке х называется предел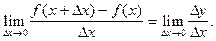

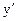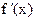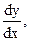Производная обозначается или , или или 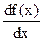и т.д.

Определение. Если производная (существует и) конечна, то функция называется дифференцируемой.

Пример 17.1. Вычислим (пользуясь определением) производную функции 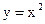. 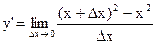=Ш= =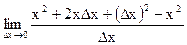

= = .

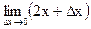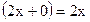Геометрический смысл производной

Теорема. Производная от функции 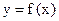в точке 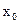равна угловому коэффициенту касательной к кривой 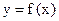, проведенной в точке 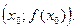Уравнение касательной имеет вид: .

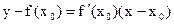Пример 18.1. Найдем уравнение касательной к графику функции 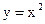в точке :

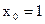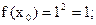
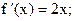
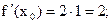уравнение касательно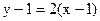й или 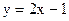(см. рис. 18.1)

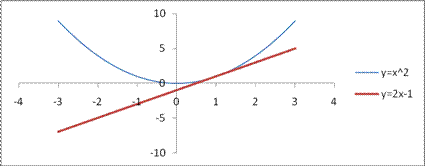
Рис. 18.1.