Матрицей размера 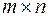 называется система
называется система 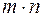 чисел, расположенных в прямоугольной таблице из
чисел, расположенных в прямоугольной таблице из 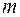 т строк и
т строк и 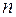 столбцов:
столбцов:
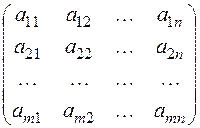 .
.
Элемент матрицы, стоящий на пересечении 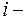 ой строки и
ой строки и 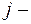 ого столбца, будем обозначать
ого столбца, будем обозначать 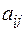 . Тогда
. Тогда 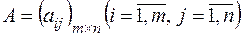 .
.
Частные случаи матриц.
1. Если 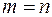 , матрица называется квадратной и
, матрица называется квадратной и  го порядка.
го порядка.
2. Если 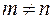 , матрица называется прямоугольной.
, матрица называется прямоугольной.
3. Если все 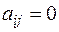 , матрица называется нулевой.
, матрица называется нулевой.
4. Квадратная матрица  называется диагональной.
называется диагональной.
5. Диагональная матрица вида 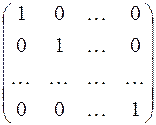 называется единичной.
называется единичной.
Каждой квадратной матрице соответствует определитель, составленный из элементов этой матрицы.
Две матрицы 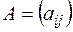 и
и 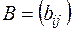 называются равными, если они имеют одинаковую размерность и равны их соответствующие элементы:
называются равными, если они имеют одинаковую размерность и равны их соответствующие элементы:
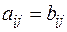 .
.
Суммой двух матриц 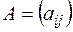 и
и 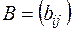 одного размера
одного размера 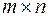 называется матрица
называется матрица 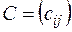 такого же размера, элементы которой равны сумме соответствующих элементов слагаемых матриц:
такого же размера, элементы которой равны сумме соответствующих элементов слагаемых матриц:
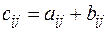 .
.
Произведением матрицы 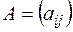 на число
на число 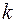 называется матрица
называется матрица 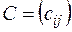 того же размера, все элементы которой равны произведению соответствующих элементов матрицы
того же размера, все элементы которой равны произведению соответствующих элементов матрицы 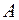 на число
на число 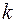 :
:
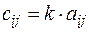 .
.
Свойства операций:
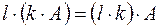 , , | 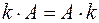 , , |
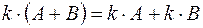 , , | 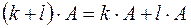 , , |
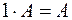 |  (матрица). (матрица). |
Две матрицы 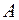 и
и 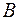 можно умножить друг на друга тогда и только тогда, когда число столбцов матрицы, стоящей первым множителем, равно числу строк матрицы, стоящей вторым множителем.
можно умножить друг на друга тогда и только тогда, когда число столбцов матрицы, стоящей первым множителем, равно числу строк матрицы, стоящей вторым множителем.
Произведением матрицы 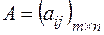 на матрицу
на матрицу 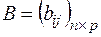 называется матрица
называется матрица 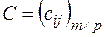 , имеющая
, имеющая 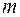 строк и
строк и 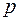 столбцов, каждый элемент которой
столбцов, каждый элемент которой 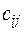 равен сумме произведений элементов
равен сумме произведений элементов 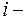 ой строки матрицы
ой строки матрицы 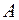 на соответствующие элементы
на соответствующие элементы 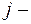 ого столбца матрицы
ого столбца матрицы 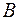 :
:
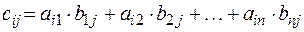 .
.
Свойства операций:
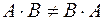 , , | 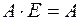 , , |
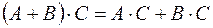 , , | 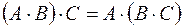 . . |
Ранг матрицы 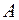 это наивысший порядок отличного от нуля минора, который можно построить из элементов данной матрицы.
это наивысший порядок отличного от нуля минора, который можно построить из элементов данной матрицы.
Ясно, что если матрица имеет размер 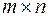 , то
, то  .
.
Если 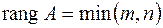 , то матрица называется неособой, в противном случае матрица называется особой или вырожденной.
, то матрица называется неособой, в противном случае матрица называется особой или вырожденной.
Квадратная матрица порядка 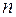 будет невырожденной, если её определитель отличен от нуля.
будет невырожденной, если её определитель отличен от нуля.
Пусть 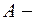 квадратная невырожденная матрица порядка
квадратная невырожденная матрица порядка 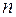 .
.
Обратной для матрицы 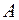 называется матрица
называется матрица 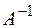 порядка
порядка 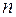 , для которой
, для которой
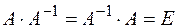 .
.
Заметим, что 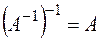 , поэтому матрицы
, поэтому матрицы 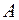 и
и 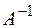 называются взаимообратными.
называются взаимообратными.
Для невырожденной матрицы  обратная матрица будет иметь вид:
обратная матрица будет иметь вид:
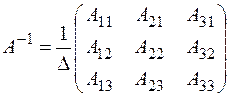 . (4)
. (4)
 2015-07-14
2015-07-14 1892
1892
