Так как для нахождения обратной матрицы важно, равен ли определитель марицы нулю или нет, то введем следующие определения.
Определение 14.9 Квадратную матрицу 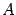 назовем вырожденной или особенной матрицей, если
назовем вырожденной или особенной матрицей, если 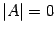 , и невырожденной или неособенной матрицей, если
, и невырожденной или неособенной матрицей, если 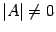 .
.
Предложение 14.21 Если обратная матрица существует, то она единственна.
Доказательство. Пусть две матрицы 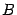 и
и 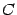 являются обратными для матрицы
являются обратными для матрицы 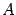 . Тогда
. Тогда
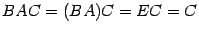 и
и 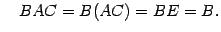
Следовательно, 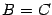 .
.
Предложение 14.22 Если квадратная матрица 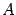 является невырожденной, то обратная для нее существует и
является невырожденной, то обратная для нее существует и
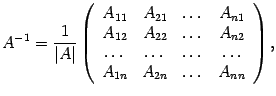 | (14.14) |
где  - алгебраические дополнения к элементам
- алгебраические дополнения к элементам 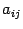 .
.
Доказательство. Так как для невырожденной матрицы 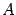 правая часть равенства (14.14) всегда существует, то достаточно показать, что эта правая часть является обратной матрицей для матрицы
правая часть равенства (14.14) всегда существует, то достаточно показать, что эта правая часть является обратной матрицей для матрицы 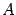 . Обозначим правую часть равенства (14.14) буквой
. Обозначим правую часть равенства (14.14) буквой 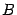 . Тогда нужно проверить, что
. Тогда нужно проверить, что 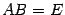 и что
и что  . Докажем первое из этих равенств, второе доказывается аналогично.
. Докажем первое из этих равенств, второе доказывается аналогично.
Пусть 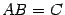 . Найдем элементы матрицы
. Найдем элементы матрицы 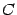 , учитывая, что
, учитывая, что 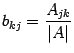 :
:
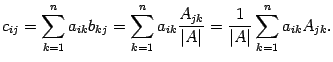
Если 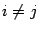 , то по предложению 14.17 сумма справа равна нулю, то есть
, то по предложению 14.17 сумма справа равна нулю, то есть 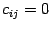 при
при 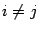 .
.
|
|
|
Если 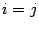 , то
, то
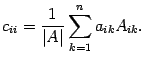
Сумма справа представляет собой разложение определителя матрицы 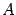 по
по 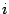 -ой строке (предложение 14.16). Таким образом,
-ой строке (предложение 14.16). Таким образом,
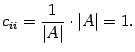
Итак, в матрице 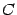 диагональные элементы равны 1, а остальные равны нулю, то есть
диагональные элементы равны 1, а остальные равны нулю, то есть 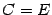 .
.
Результаты предложений 14.20, 14.21, 14.22 соберем в одну теорему.
Теорема 14.1 Обратная матрица для квадратной матрицы 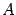 существует тогда и только тогда, когда матрица
существует тогда и только тогда, когда матрица 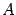 - невырожденная, обратная матрица единственна, и справедлива формула (14.14).
- невырожденная, обратная матрица единственна, и справедлива формула (14.14).
Замечание 14.12 Следует обратить особое внимание на места, занимаемые алгебраическими дополнениями в формуле обратной матрицы: первый индекс показывает номер столбца, а второй - номер строки, в которые нужно записать вычисленное алгебраическое дополнение.
Пример 14.7 Найдите обратную матрицу для матрицы 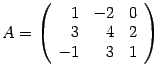 .
.
Решение. Находим определитель
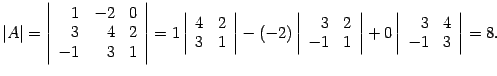
Так как 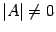 , то матрица
, то матрица 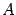 - невырожденная, и обратная для нее существует.
- невырожденная, и обратная для нее существует.
Находим алгебраические дополнения:
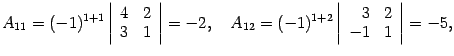
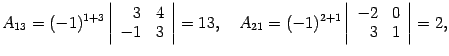
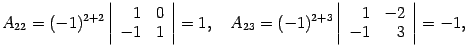
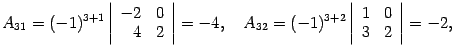
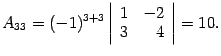
Составляем обратную матрицу, размещая найденные алгебраические дополнения так, чтобы первый индекс соответствовал столбцу, а второй - строке:
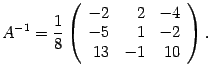 | (14.15) |
Полученная матрица и служит ответом к задаче.
Замечание 14.13 В предыдущем примере было бы точнее ответ записать так:
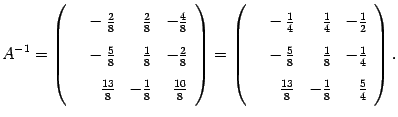 | (14.16) |
Однако запись (14.15) более компактна и с ней удобнее проводить дальнейшие вычисления, если таковые потребуются. Поэтому запись ответа в виде (14.15) предпочтительнее, если элементы матриц - целые числа. И наоборот, если элементы матрицы 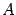 - десятичные дроби, то обратную матрицу лучше записать без множителя
- десятичные дроби, то обратную матрицу лучше записать без множителя 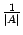 впереди.
впереди.
Замечание 14.14 При нахождении обратной матрицы приходится выполнять довольно много вычислений и необычно правило расстановки алгебраических дополнений в итоговой матрице. Поэтому велика вероятность ошибки. Чтобы избежать ошибок следует делать проверку: вычислить произведение исходной матрицы на итоговую в том или ином порядке. Если в результате получится единичная матрица, то обратная матрица найдена правильно. В противном случае нужно искать ошибку.
|
|
|
Пример 14.8 Найдите обратную матрицу для матрицы 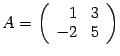 .
.
 2015-01-30
2015-01-30 12361
12361
