Решение систем линейных уравнений с помощью определителей удобно производить для систем двух или трёх уравнений. В случае же систем большего числа уравнений удобнее пользоваться методом Гаусса, который заключается в последовательном исключении неизвестных.
Пусть задана система 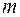 линейных уравнений с
линейных уравнений с 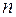 неизвестными:
неизвестными:
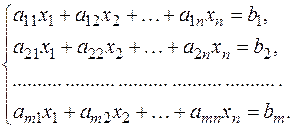
Обозначим 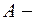 матрицу системы,
матрицу системы, 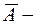 расширенную матрицу системы:
расширенную матрицу системы:
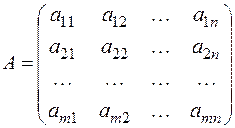 ,
, 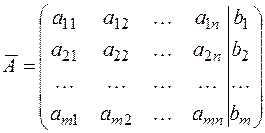 .
.
Умножение какого-либо уравнения системы на число и прибавление к другому уравнению не меняет системы. Используя этот факт, преобразуем расширенную матрицу системы к следующему виду: в первом столбце все элементы, начиная со второго равны нулю; во втором столбце все элементы, начиная с третьего равны нулю; в третьем— начиная с четвёртого и т.д. В результате матрица приводится к ступенчатому виду.
Возможны три основные случая:
1) 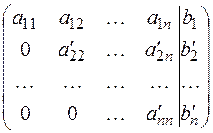
Матрица имеет треугольный вид (число неизвестных равно числу линейно независимых уравнений), система имеет единственное решение. Записываем систему, соответствующую преобразованной матрице, из последнего уравнения находим 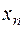 , подставляем в предпоследнее уравнение и находим
, подставляем в предпоследнее уравнение и находим 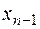 , затем
, затем 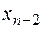 и т. д.
и т. д.
2) 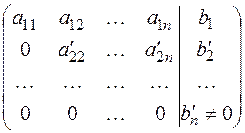 .
.
Система содержит хотя бы одно уравнение вида 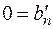 , система не имеет решений.
, система не имеет решений.
3) 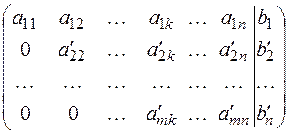 .
.
Матрица не треугольная, так как последнее уравнение содержит более одного неизвестного, система имеет бесконечно много решений.
Задача 13. Решить систему методом Гаусса
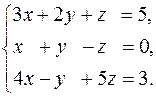
Решение. Выпишем расширенную матрицу системы и преобразуем её:
1) поменяем местами первую и вторую строки:
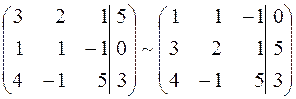 ;
;
2) прибавим ко второй строке первую, умноженную на 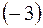 , а к третьей
, а к третьей 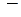 первую, умноженную на
первую, умноженную на 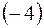 :
:
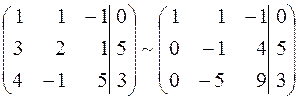 ;
;
3) прибавим к третьей строке вторую, умноженную на 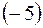 :
:
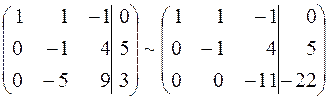 .
.
Система уравнений приняла треугольный вид:
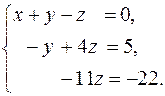
Она имеет единственное решение. Из последнего уравнения 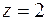 , подставляя это значение во второе уравнения, получаем
, подставляя это значение во второе уравнения, получаем 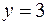 . Из первого уравнения находим
. Из первого уравнения находим 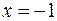 .
.
Задача 14. Решить систему методом Гаусса
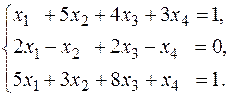
Решение. Выпишем расширенную матрицу системы и преобразуем её:
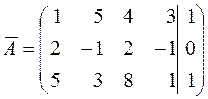 .
.
1) Прибавим ко второй строке первую, умноженную на 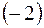 , а к третьей
, а к третьей 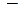 первую, умноженную на
первую, умноженную на 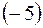 , получим
, получим
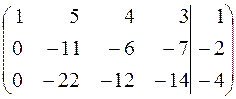 .
.
2) Прибавим к третьей строке вторую, умноженную на 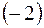 :
:
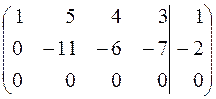 .
.
Матрица приведена к ступенчатому виду, и последнее уравнение содержит несколько неизвестных. Следовательно, система имеет бесконечно много решений.
Первое и второе уравнение преобразованной системы и перепишем в виде:
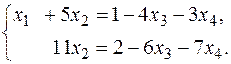
Выразим неизвестные 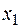 и
и 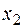 через
через  и
и 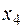 :
:
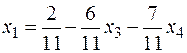 ,
, 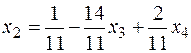 .
.
Придавая  и
и 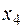 различные числовые значения, будем получать различные решения данной системы.
различные числовые значения, будем получать различные решения данной системы.
 2015-07-14
2015-07-14 1029
1029








