Пусть задана система трёх линейных уравнений с тремя неизвестными:
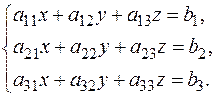
Введём обозначения 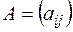 ,
, 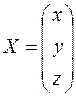 ,
,  . Тогда систему
. Тогда систему
можно записать в матричном виде:
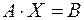 .
.
Пусть определитель матрицы 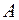 не равен нулю (
не равен нулю (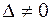 ). Следовательно, существует обратная матрица
). Следовательно, существует обратная матрица 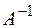 . Тогда решение системы имеет вид
. Тогда решение системы имеет вид
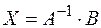 .
.
Задача 7. Вычислить 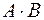 и
и 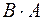 , если
, если
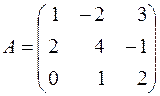 ,
, 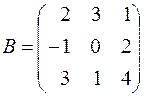 .
.
Решение. Матрицы имеют размер 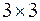 . Это означает, что произведение матриц можно вычислить и результат также будет матрицей
. Это означает, что произведение матриц можно вычислить и результат также будет матрицей 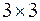 .
.
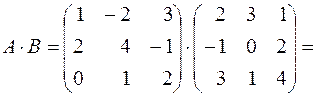
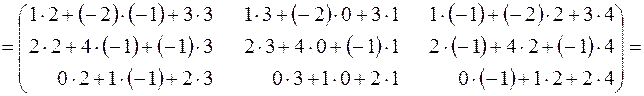
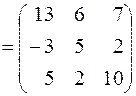 .
.
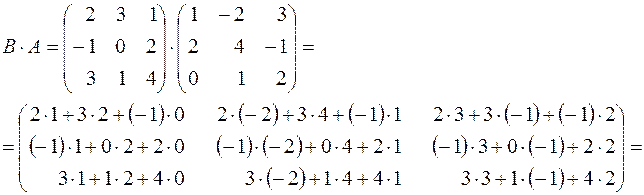
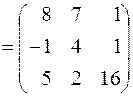 .
.
Задача 8. Найти ранг матрицы 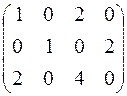 .
.
Решение. Первый способ. Вычислим ранг матрицы по определению: найдём наивысший порядок минора, отличного от нуля.
Найдём хотя бы один минор второго порядка отличный от нуля. Например, минор второго порядка 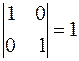 .
.
Найдём хотя бы один минор третьего порядка отличный от нуля.
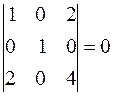 ,
, 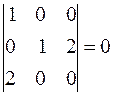 ,
, 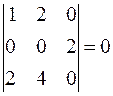 ,
,  .
.
Все миноры третьего порядка равны нулю, следовательно, наивысший порядок минора, отличного от нуля, равен 2. Это означает, что ранг данной матрицы равен 2.
Второй способ. Следующие элементарные преобразования не меняют ранга матрицы:
1) умножение строки или столбца на число не равное нулю;
2) прибавление строки или столбца к другой строчке или столбцу;
3) вычёркивание нулевой строки или столбца.
Выполним следующие преобразования матрицы:
1) разделим третью строку на 2:
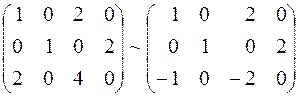 ;
;
2) прибавим к третьей строке первую:
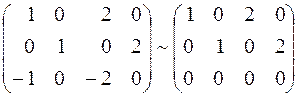 ;
;
3) вычеркнем третью нулевую строку:
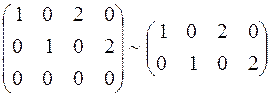 .
.
Отсюда видно, что наивысший порядок минора отличного от нуля равен двум, и, следовательно, ранг данной матрицы равен 2.
Задача 9. Решить систему уравнений в матричной форме
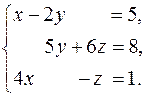
Решение. Перепишем систему в матричном виде 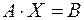 , где
, где
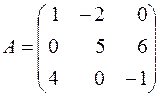 ,
, 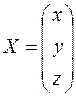 ,
, 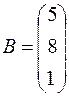 .
.
Решение матричного уравнения имеет вид:
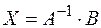 .
.
Найдём обратную матрицу 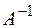 . Для этого вычислим определитель матрицы
. Для этого вычислим определитель матрицы 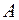 :
:
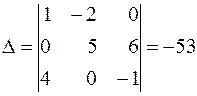 .
.
Далее, вычислим алгебраические дополнения элементов этого определителя:
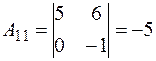 , , | 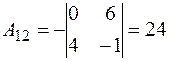 , , | 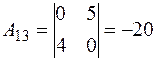 , , |
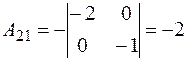 , , | 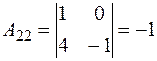 | 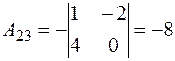 |
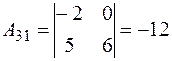 | 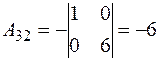 | 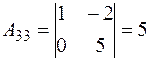 . . |
Таким образом, по формуле (4) обратная матрица имеет вид:
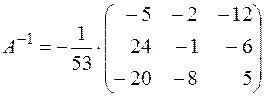 .
.
Тогда
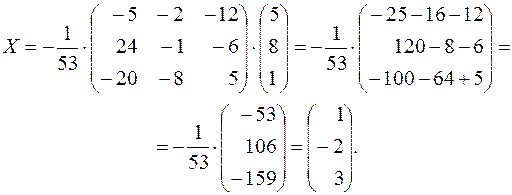
Следовательно, 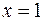 ,
, 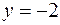 ,
, 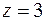 .
.
 2015-07-14
2015-07-14 2867
2867
