Складання та моделювання гідравлічних і теплових ОБ’ЄКТІВ (6 год.)
І. Мета роботи
Мета даної роботи - освоїти прийоми моделювання в середовищі Matlab гідравлічних об’єктів.
2 КОРОТКІ ТЕОРЕТИЧНІ ВІДОМОСТІ
Опис об'єктів моделювання включає три стадії: першу (основну) - побудову моделі; другу - попередню роботу з нею; третю - корекцію і зміну за результатами попередньої роботи.
Найбільш складною і відповідальною є перша стадія. Часто це досить довгий шлях, проходити який доводиться методом проб і помилок. Побудова принципово нової математичної моделі носить характер наукового відкриття.
При математичному описі об'єктів моделювання основною задачею є одержання диференціальних рівнянь окремих елементів, з яких складається вихідний об'єкт. Рівняння окремих елементів складаються на основі тих фізичних законів, які характеризують роботу певного елементу. Ними можуть бути закони механіки, електротехніки, теплотехніки, оптики та ін.
Після того, як математична модель отримана, наступає другий етап спрощення (ідеалізації). Аналізують всі складові моделі і якщо виявиться, що деякі члени моделі за своїм значенням значно менші від інших членів моделі (при можливих режимах роботи об'єкта), то такими членами нехтують. В теорії керування с особлива форма ідеалізації, яка називається лінеаризацією. Суть якої в тому, що нелінійні функції, які входять в диференціальні рівняння розкладають в ряд Тейлора, обмежившись лише лінійними членами такого ряду.
Залежно від конкретної задачі, яку розв'язує дослідник, математичну модель об’єкта необхідно подати в тій чи іншій формі. У практиці керування лінеризовані математичні моделі подаються у формі диференціальних рівнянь, передавальних функцій, в формі системи диференціальних рівнянь (в просторі станів), в матрично-векторній формі і в формі матричних передавальних функцій.
Подання математичної моделі в просторі станів. Для розв'язку цілого ряду задач - моделювання на цифрових ЕОМ, оптимізації, "аналітичного" конструювання регуляторів та інше - застосовують опис об'єктів у просторі станів
Такий опис виникає природнім шляхом при моделюванні багатовимірних об'єктів або в результаті заміни диференціального рівняння n–го порядку системою диференціальних рівнянь. Таку заміну можна здійснити декількома способами.
Перший спосіб. Цей спосіб можна застосувати в тому випадку, коли права частина диференціального рівняння не вмішує похідних. В такому випадку маємо
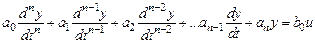 . (10.1)
. (10.1)
Якщо розв’язати рівняння відносно старшої похідної та провести незначні перетворення, отримаємо
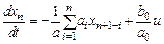 . (10.2)
. (10.2)
Другий спосіб. Розклад на елементарні дроби.
Третій спосіб. Розглянемо диференціальне рівняння
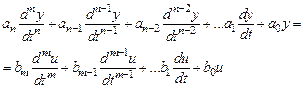 . (10.3)
. (10.3)
в якому m = n. Якщо це не так, то, прирівнюючи до нуля коефіцієнти bm+1bm+2,…bn, завжди зможемо записати рівняння (10.3) у вигляді
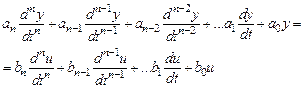 . (10.4)
. (10.4)
Рівняння (10.4) розпадається на систему диференціальних рівнянь першого порядку
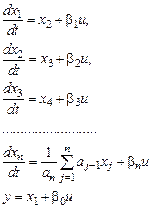 (10.5)
(10.5)
Цей спосіб є найуніверсальнішим, оскільки він не накладає ніяких обмежень на порядок похідної в правій частині диференціального рівняння (10.4)
Передавальні матричні функції дають можливість описати динаміку багатовимірного об'єкта системи в частотній області. Для систем (об'єктів), які мають більше однієї вхідної величини вводять поняття матричної передавальної функції.
Нехай система має т входів і п виходів.
Тоді матричною передавальною функцією називають матрицю розміром n х m, елементами якої є передавальні функції W(p), що визначаються як відношення і-і вихідної величини, до j-ї вхідної, перетворених за Лапласом при нульових початкових умовах.
Матрично-векторна форма математичної моделі. До цієї форми рівнянь звертаються тоді, коли пригодиться моделювати системи з багатьма входами і виходами (багатовимірні системи). В такому випадку повний опис цього класу систем вимагає великої кількості інформації. Цю інформацію, яка складається із систем диференціальних рівнянь, зручно подати у вигляді матриць. Тоді аналіз системи зводиться, як правило, до аналізу властивостей матриць.
Нехай лінеаризована математична модель об’єкта (системи) подана у вигляді системи диференціальних рівнянь
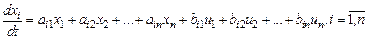 , (10.6)
, (10.6)
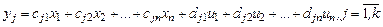 ,(10.7)
,(10.7)
Введемо матриці
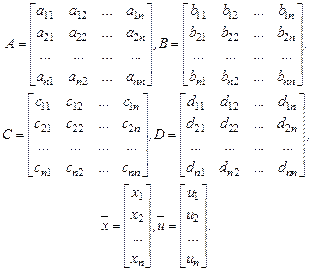
Тоді системи рівнянь (10.6) і (10.7) запишемо в такому вигляді:
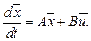 (10.8)
(10.8)
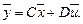 (10.9)
(10.9)
Розглянемо приклад побудови математичної моделі гідравлічного об'єкта та обчислення її параметрів.
В ємність (рис. 10.1) поступає рідина з відомою масовою витратою q1; витрата рідини, яка витікає із ємності q2. Необхідно знайти зміну рівня H(t) для будь-якого моменту часу t в залежності від зміни витрати q1 на вході в ємність (див. рис. 10.1).
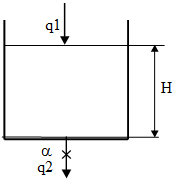
Рисунок 10.1- Схема гідравлічного об'єкта
Математичну модель ємності будемо складати при таких допущеннях:
а) густина рідини ρ = const і не залежить від температури;
б) поперечний переріз в ємності S стале і не змінюється з висотою;
г) випаровуванням рідини нехтуємо.
Основним фізичним законом, який обумовлює динаміку об'єкта, є рівняння матеріального балансу, що має такий вигляд:
[Швидкість накопичення рідини]=[Притік]-[Стік]. (10.10)
Швидкість накопичення рідіти - це зміна маси рідини в часі, тобто 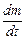 . Якщо площа поперечного перерізу S, а рівень рідини Н, то маса рідини т = Vρ= SHρ. Тоді
. Якщо площа поперечного перерізу S, а рівень рідини Н, то маса рідини т = Vρ= SHρ. Тоді
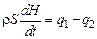 .
.
При вільному витіканні рідини із ємності
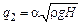 .
.
Де 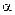 - місцевий гідравлічний опір. Отже:
- місцевий гідравлічний опір. Отже:
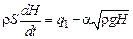 . (10.11)
. (10.11)
Рівняння (10.11) відтворює зміну рівня рідини в ємності при зроблених допущеннях (ідеалізації). Воно нелінійне. Якщо відхилення рівня від рівноважного стану невелике, то рівняння (10.11) можна лінеаризувати. Нехай 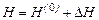 і
і 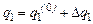 . В рівноважному стані
. В рівноважному стані 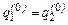 . Тоді
. Тоді
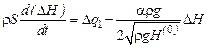 . (10.12)
. (10.12)
Якщо ввести позначення 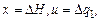
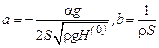 , то рівняння динаміки ємності набуде стандартного вигляду
, то рівняння динаміки ємності набуде стандартного вигляду
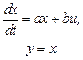 (10.13)
(10.13)
Єдиним параметром математичної моделі, який необхідно визначити, є гідравлічний опір α. Його ми обчислимо, розглянувши статичний режим роботи об'єкта, який має місце тоді, коли рівень рідини сталий.
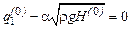 . (10.14)
. (10.14)
З рівняння (10.14) знаходимо
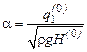 . (10.15)
. (10.15)
Моделювання об’єктів будемо виконувати в Matlab, використовуючи засоби Simulink.
 2015-07-14
2015-07-14 511
511








