Рассмотрим функцию y = sin x2.
Чтобы найти значение этой функции в фиксированнной точке x нужно: 1) вычислить x2; 2) найти значение синуса от полученного значения x2.
Иными словами, сначала надо найти значение g (x) = x2, а потом найти sin g (x).
В подобных случаях говорят, что задана сложная функция y = f (g (x)).
В нашем примере u = g (x) = x2, а y = f (u) = sin u.
Пусть y = f (g (x)) - сложная функция, причем функция u = g (x) дифференцируема в точке x, а функция y = f (u) дифференцируема в соответствующей точке u.
Тогда функция y = f (g (x)) дифференцируема в точке x,
причем y  = f
= f  (g (x))
(g (x))  g
g  (x).
(x).
Запись f '(g (x)) означает, что производная вычисляется по формуле для f '(x), но вместо x подставляется g (x).
2.Таблица основных производных
| Функция y = f (x) | Производные элементарных функций простого аргумента | Функция y = f (kx +b) | Производные элементарных функций сложного аргумента |
| y = xn | y  = n = n  xn −1 xn −1 | y =(kx + b) n | y  = n = n  k k  (kx + b) n −1 (kx + b) n −1 |
| y = x | y  =1 =1 | y =(kx + b) | y  = k = k |
y = 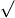 x x | y  =12 =12 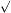 x x | y = 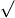 kx + b kx + b | y  = k = k  12 12 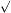 kx + b kx + b |
| y = x 1 | y  =−1 x 2 =−1 x 2 | y =1 kx + b | y  =− k =− k  1(kx + b)2 1(kx + b)2 |
| y = cos x | y  =− sinx =− sinx | y = cos (kx +b) | y  =− ksin (kx + b) =− ksin (kx + b) |
| y = sin x | y  = cosx = cosx | y = sin (kx +b) | y  = kcos (kx + b) = kcos (kx + b) |
| y = tg x | y  =1 cos 2 x =1 cos 2 x | y = tg (kx +b) | y  = k = k  1 cos 2(kx + b) 1 cos 2(kx + b) |
| y = ctg x | y  =−1 sin 2 x =−1 sin 2 x | y = ctg (kx +b) | y  =− k =− k  1 sin 2(kx + b) 1 sin 2(kx + b) |
| y = arcsin x | y  =1 =1 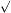 1− x 2 1− x 2 | y = arcsin (kx +b) | y  = k = k  1 1 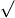 1−(kx + b)2 1−(kx + b)2 |
| y = arccos x | y  =−1 =−1 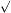 1− x 2 1− x 2 | y = arccos (kx +b) | y  =− k =− k  1 1 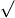 1−(kx + b)2 1−(kx + b)2 |
| y = arctg x | y  =11+ x 2 =11+ x 2 | y = arctg (kx +b) | y  = k = k  11+(kx + b)2 11+(kx + b)2 |
| y = arcctg x | y  =−11+ x 2 =−11+ x 2 | y = arcctg (kx +b) | y  =− k =− k  11+(kx + b)2 11+(kx + b)2 |
y = ax  a a 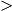 0 0  a a  =1 =1 | y  = ax = ax  lna lna  a a 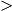 0 0  a a  =1 =1 | y = akx + b  a a 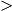 0 0  a a  =1 =1 | y  = k = k  akx + b akx + b  lna lna  a a 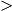 0 0  a a  =1 =1 |
| y = ex | y  = ex = ex | y = ekx + b | y  = k = k  ekx + b ekx + b |
y = logax  a a 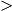 0 0  a a  =1 =1 | y  =1 x =1 x  lna lna | y = loga (kx + b)  a a 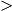 0 0  a a  =1 =1 | y  = k = k  1(kx + b) 1(kx + b)  lna lna |
| y = lnx | y  = x 1 = x 1  x x 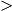 0 0 | y = ln (kx +b) | y  = k = k  1 kx + b 1 kx + b  kx + b kx + b 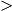 0 0 |
3. Нахождение промежутков возрастания, убывания, точки экстремума
 2015-07-14
2015-07-14 1036
1036