2015-07-14
3498
М атериальная точка может совершать колебания как вдоль оси х, так и вдоль перпендикулярной к ней оси у. Если возбудить оба колебания, материальная точка будет двигаться по некоторой, вообще говоря, криволинейной траектории, форма которой зависит от разности фаз обоих колебаний.
Выберем начало отсчета времени так, чтобы начальная фаза первого колебания была равна нулю. Тогда уравнения колебаний запишутся следующим образом:
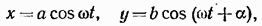
где — разность фаз обоих колебаний.
Выражения (57.1) представляют собой заданное в параметрической форме уравнение траектории, по которой движется тело, участвующее в обоих колебаниях. Чтобы получить уравнение траектории в обычном виде, нужно исключить из уравнений (57.1) параметр t. Из первого уравнения следует, что
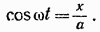
Следовательно,
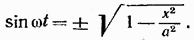
Фигу́ры Лиссажу́ — замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях.
Дифференциальное уравнение затухающих колебаний и его решение. Основные параметры затухающих колебаний. Изменение характера затухающих колебаний с ростом коэффициента трения. Добротность.
|
|
|
Затухающие колебания — колебания, амплитуды которых из-за потерь энергии реальной колебательной системой с течением времени уменьшаются.
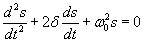
Дифференциальное уравнение свободных затухающих колебаний линейной системы
