Глава 12. Дифференциальные уравнения
12.1. Основные понятия
Краткая теория
Дифференциальным уравнением называется уравнение, связывающее независимую переменную х, искомую функцию у = f (x) и ее производные различных порядков.
Порядком дифференциального уравнения называется порядок старшей производной, входящей в это уравнение.
Дифференциальное уравнение n-го порядка в общем виде записывается так:
F (x,y,y',y'',... y (n)) = 0.
Решением дифференциального уравнения называется любая функция y = φ (x),
обращающая это уравнение в тождество.
Решение F (x,y) = 0, заданное в неявном виде, называется интегралом дифференциального уравнения.
График решения дифференциального уравнения называется интегральной кривой.
Общим решением дифференциального уравнения n - го порядка называется функция
у = φ (х,С1,С2,...,Сn),
зависящая от х и n произвольных независимых постоянных С1,С2,...,Сn, обращающая это уравнение в тождество.
Общее решение, заданное в неявном виде
Ф (х,y,С1,С2,...,Сn) = 0,
называется общим интегралом.
Частным решением дифференциального уравнения называется решение, которое получается из общего, если придать определенные значения произвольным постоянным, т.е. решение вида:
у = φ (х,С01,С02,...,С0n),
где С01,С02,...,С0n - фиксированные числа.
Частным интегралом называется интеграл, полученный из общего путем
фиксирования произвольных постоянных:
Ф (х,y,С01,С02,...,С0n) = 0,
где С01,С02,...,С0n - фиксированные числа.
Дифференциальные уравнения первого порядка.
Краткая теория
Общий вид дифференциального уравнения первого порядка:
F (x,у,у') = 0. (12.1)
Если это уравнение разрешимо относительно у', то
у' = f(х,у) или dу = f(x,y)dx. (12.2)
Это уравнение можно записать так:
P(x,y)dx + Q(x,y)dy = 0. (12.3)
Общим решением уравнения (12.1) называется функция
y = φ(x,C) (12.4)
от х и произвольной постоянной С, обращающая это уравнение в тождество.
Общее решение, заданное в неявном виде
Ф (x,y,C) = 0, (12.5)
называется общим интегралом.
Геометрически общее решение (и общий интеграл) представляет собой семейство интегральных кривых на плоскости, зависящих от одного параметра С.
Частным решением уравнения (12.1) называется решение, полученное из общего решения (12.4) при фиксированном значении С:
y = φ(x,C0) (12.6)
где C0 - фиксированное число.
Частным интегралом уравнения (1) называется интеграл, полученный из общего интеграла (5) при фиксированном значении С:
Ф (x,y,C0) = 0. (12.7)
Задача Коши. Найти решение у = f (х) дифференциального уравнения (1), удовлетворяющее заданным начальным условиям: у = y 0 при х = х 0.
Другими словами: найти интегральную кривую уравнения (1), проходящую через данную точку М0 (х0,y0).
Дифференциальные уравнения с разделяющимися переменными.
Краткая теория
Дифференциальным уравнением с разделяющимися переменными называется уравнение вида
Х(x)Y(y)dx + X1(x)Y1(y)dy = 0, (12.8)
где X(x), X1(x) - функции только от х; Y(y), Y1(y) – функции только от у.
Уравнение (12.8) делением на произведение Y(y) X1(x) приводится к уравнению с разделенными переменными:
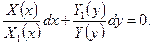 (12.9)
(12.9)
Общий интеграл уравнения (12.9)
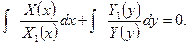 (12.10)
(12.10)
Замечание. При делении на произведение Y(y) X1(x)  можно потерять те решения уравнения (12.8), которое обращают это произведение в нуль.
можно потерять те решения уравнения (12.8), которое обращают это произведение в нуль.
Непосредственной подстановкой легко убедиться, что функция x = a, где а есть корень уравнения X1(x) = 0, т.е. X1(a) = 0, является решением уравнения (12.8). Функция y = b, где b корень уравнения Y1(y) = 0, т.е. Y1 (b) = 0, также является решением уравнения (12.8). Решения x = a и x = b, если они имеются, геометрически представляют собой прямые линии, соответственно параллельные оси Oy и оси Ox.
1. Проинтегрировать дифференциальное уравнение
(1+x2) dy - 2xy dx = 0.
Найти частное решение, удовлетворяющее условию: y = 1 при x = 0.
Данное уравнение является уравнением с разделяющимися переменными (коэффициент при dy - функция только от х, при dx – произведение функций, одна из которых зависит только от х, другая - только от у). Разделив обе части уравнения на произведение у (1+x2), получим уравнение с разделенными переменными
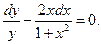
Интегрируя это уравнение, находим
ln |y| - ln (1+x2) = ln |C| или 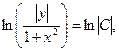
откуда получаем общее решение: у = C (1+x2).
Чтобы найти искомое частное решение, достаточно определить значение С по начальным условиям: 1 = C (1+0), C = 1.
Следовательно, частное решение имеет вид
у = 1+ x2.
Замечание. При делении на y(1 + x2) предполагалось, что y(1+x2) ≠ 0, т.е. y ≠ 0, 1+x2 ≠ 0. Но у = 0 - решение уравнения, в чем можно непосредственно убедиться. Это решение получается из общего при С = 0.
2. Найти общий интеграл дифференциального уравнения
(xy2 + x)dx + (y - x2 y)dy = 0.
Вынося соответствующие множители за скобки, данное уравнение можно
записать так: x(y2+1)dx + y(1 - x2)dy = 0,
откуда видно, что это уравнение с разделяющимися переменными. Разделив обе части последнего уравнения на произведение (y2 + 1)(1 - x2) ≠ 0, получим
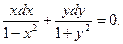
Интегрируя это уравнение, находим
- ln |1- x2| + ln |1 + y2| = ln |C| или 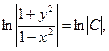
откуда получаем общий интеграл: 1 + y2 = C(1 - x2).
Проинтегрировать дифференциальные уравнения, найти указанные частные решения и построить их:
12.1. 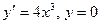 при
при 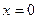 .
.
12.2. 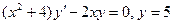 при
при 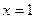 .
.
12.3. 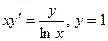 при
при 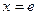 .
.
12.4. 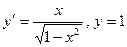 при
при 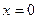 .
.
12.5. 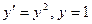 при
при 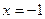 .
.
12.6. 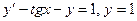 при
при 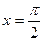 .
.
Проинтегрировать дифференциальные уравнения с разделяющими переменными:
12. 7. 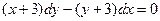 12. 8.
12. 8. 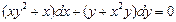 . 12.9.
. 12.9. 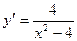 .
.
12.10. 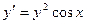 . 12.11.
. 12.11. 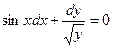 . 12.12.
. 12.12. 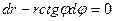 .
.
 2015-03-22
2015-03-22 14153
14153