Пример 2.3

Определить скорость и ускорение звена 5 механизма изображенного на рисунке 2.5,а в положении, когда w₁=135°.

Размеры звеньев механизма заданы:

l_ОА = 0,06 м; l_AB = 0,12 м; 1_BC = 0,08 м; x₁ = 0,054 м; у = 0,056 м;

х₂ = 0,087 м. Частота вращения кривошипа известна: n = 190 об/мин.

Решение.

Выполняем структурный анализ механизма. Число степеней свободы механизма:

W = 3n–2p5–p4 =3·5–2·7= 1.

Следовательно, в механизме одно входное звено (один механизм I класса).

Структурная формула механизма: I (0,1)→II(2,3)→II(4,5).

Согласно структурной формуле последовательность кинематического анализа следующая:

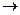А С В D₃ Е₀ D₅,

где т. А – конец кривошипа;

т.т. А,С – внешние точки диады 2,3, т. В – внутренняя;

D₃ и Е₀ – внешние точки диады 4,5, т. D₅ – внутренняя.

В такой последовательности будем строить план положения механизма методом засечек.

Принимаем ОА = 30 мм. Тогда

.

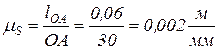Коэффициент длин стандартный и соответствует чертежному масштабу М1:2.

Построение плана скоростей начинаем с определения скорости конца кривошипа т. А:

^.

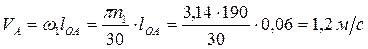Эту скорость изображаем отрезком 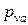= 60мм.

Тогда масштабный коэффициент скоростей

^.

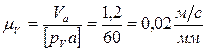Коэффициент стандартный. Вектор 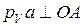, т.к. кривошип вращается, и направлен в сторону его вращения.

Переходим к диаде (2,3). Т. А является внешней точкой этой диады, а скорость т. С Vc = 0, т.к. точка неподвижна. Тогда можно рассмотреть скорость движения внутренней точки диады (т. В), соединяющей звенья этой диады, по отношению к внешним точкам диады и запишем два векторных уравнения:

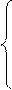
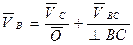^{, (2.5)}

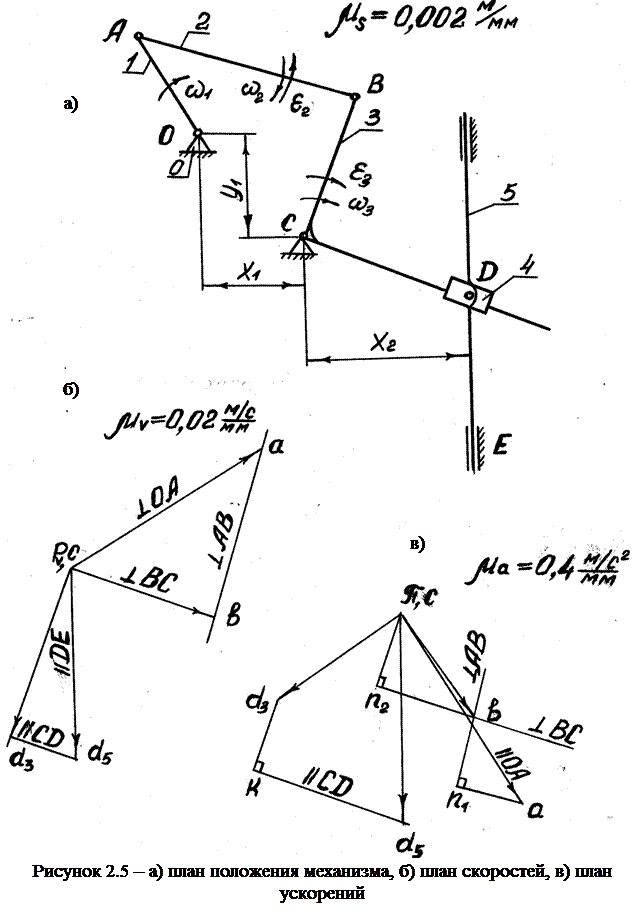где 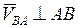, т.к. обе точки принадлежат одному и тому же звену 2, которое имеет плоскопараллельное движение; 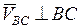т. к звено 3 имеет вращательное движение. Уравнения (2.5) решаем графически. Согласно первому уравнению через точку «а» проводим прямую 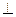к АВ, а согласно второму уравнению, через полюс « 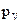» проводим перпендикуляр к ВС. На пересечении перпендикуляров получим точку «b».

Для нахождения 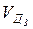удобно воспользоваться свойством подобия, согласно которому

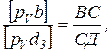откуда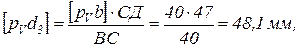

где 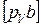замеряют в мм на плане скоростей, а СД – в мм на плане положения механизма.

Переходим к группе Ассура (4,5). В ней известны скорости точек Д₃ и Е₀, расположенной на стойке. Точка Д₅ – центр шарнира является внутренней точкой диады (4,5). Рассмотрим движение этой точки по отношению к т. Д₃, а затем т. Е₀ и запишем два векторных уравнения:

(2.6)

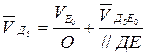
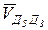║СД, т.к. Т. Д₃ принадлежит звену 3, а т. Д₅ – одновременно звеньям 4 и 5, т.к. вращательная пара соединяет эти звенья, т.е. т. Д₃ – это точка кулисы, а т. Д₅ точка кулисного камня, а кулисный камень по кулисе движется поступательно прямолинейно. 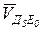║‌‌ДЕ, т.к. ползун 5 относительно стойки движется поступательно прямолинейно. Поэтому на плане скоростей из т. d₃ проводим прямую параллельно СД, а т.к. V_Е = 0, то из т. «p_v» – прямую ║ ДЕ и на пересечении этих линий получим точку «d₅».

Умножая отрезки на плане скоростей на масштабный коэффициент 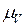, определяем величины скоростей. Причем векторы, идущие из полюса p_V, изображают абсолютные скорости, а отрезки, соединяющие концы этих векторов – относительные скорости точек.

Получаем:

^,

^,

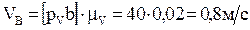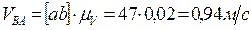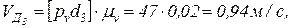
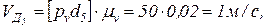
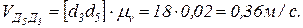
Вычисляем модули угловых скоросте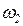й и 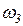звеньев 2 и 3:

^,

^.

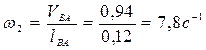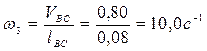Направление 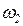определяем, перенося вектор 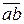направленный от точки «а» к точке «b» (по правилу сложения векторов в первом уравнении системы (2.5)) в т. В звена и рассматривая движение т. В относительно т. А в направлении 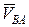(по часовой стрелке). Направление 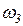определяем, перенося вектор 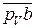в т. В звена 3 и рассматривая движение т. В относительно т. С в направлении этого вектора (так же по часовой стрелке).

Последовательность построения плана ускорений точно такая же, как и плана скоростей.

Так как кривошип вращается равномерно, то.

^.

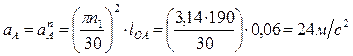Изображаем это ускорение отрезком 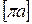= 60мм. Тогда масштабный коэффициент ускорений 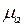будет соответствовать рекомендуемым значениям

^.

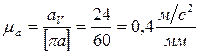Так как ускорение а_А состоит только из нормального (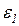 = 0),то вектор 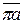направляем по звену ОА к точке О (рис. 2.5). Это план ускорений кривошипа.

Рассматриваем структурную группу (2,3). В ней известны ускорения внешних точек диады (т. А и т. С). Составим для определения а_B систему двух векторных уравнений, в которых рассмотрим движение т. В сначала относительно т. А, а затем по отношению к т. С.

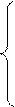
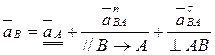(2.7)

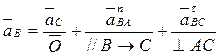
Направления векторов в уравнениях (2.7) записаны исходя из того, что звено 2 имеет плоскопараллельное движение (первое уравнение), а звено 3 –вращательное (второе уравнение).

Вычислим величины нормальных составляющих ускорений:

^,

^.

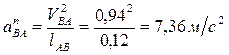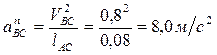Нормальные составляющие ускорений представим в виде отрезков:

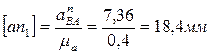
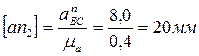
В соответствии с первым уравнением из точки «а» в направлении от В к А откладываем отрезок 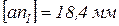, из конца которого проводим линию AB. Согласно второму уравнению их точки «π» плана в направлении от т. В к т. С откладываем отрезок 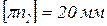и из точки «» проводим линию ВС. На пересечении перпендикуляров получим точку «b».

Ускорение точки Д₃ находим, используя свойство подобия и сходственности расположения относительных ускорений точек звена 3.

Согласно этому свойству составим пропорцию:

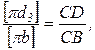
^откуда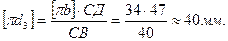

Отрезок 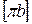замеряем на плане ускорений, а СД – на плане положения механизма.

Фигура ВСД на звене должна быть сходственно расположена с фигурой на плане ускорений 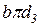(обход точек против хода часовой стрелки).

Теперь рассмотрим структурную группу (4,5). Рассуждая аналогично с построением плана скоростей группы, запишем два векторных уравнения, в которых ускорение внутренней точки диады выражается при рассмотрении ее движения относительно внешних точек диады:

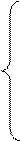
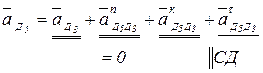(2.8)

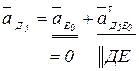
В первом уравнении описывается движение кулисного камня (т. Д₅) относительно кулисы 3 (т. Д₃). Т.к. в первом уравнении описывается сложное движение т. Д₅, которое состоит из относительного движения кулисного камня по кулисе и переносного движения т. Д₃ кулисы 3 относительно неподвижной т. С. В данном механизме переносное движение (движение кулисы) вращательное. Следовательно, возникнет ускорение Кориолиса 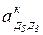, которое определяется по формуле

^,

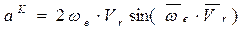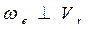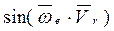^{т.к. , то =1.}

Тогда применительно к кулисному механизму, ускорение Кориолиса определяется как удвоенное произведение угловой скорости кулисы на скорость относительного движения кулисного камня по кулисе.

Следовательно,

^.

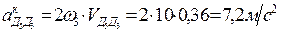На плане ускорений ускорение Кориолиса 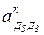изобразится в виде отрезка 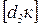, величина которого определится по формуле

^.

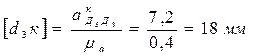Направление ускорения Кориолиса определится по правилу Жуковского, согласно которому вектор относительной скорости кулисного камня по кулисе нужно повернуть на 90° в сторону вращения кулисы.

В данном примере вектор на плане скоростей 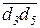, который по правилу сложения векторов направлен от точки «d₃» к точке «d₅», нужно повернуть па 90° по часовой стрелке (направление 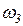). Поэтому ускорение 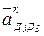будет направлено вниз 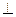СД.

Решаем векторные уравнения (2.8) графически. В соответствии с первым уравнением из точки «d₃» 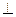СД вниз откладываем отрезок [d₃к], из конца которого проводим линию ║СД. В этом уравнении 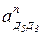=0, т.к. движение кулисного камня по кулисе прямолинейное. Согласно второму уравнению системы (2.8) из полюса плана «π» проводим линию ║ДЕ. На пересечении двух линий первого и второго уравнений получим точку «d₅». План ускорений построен. Из этого плана определяем величины абсолютных ускорений точек звеньев:

^,

^,

^.

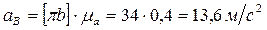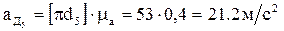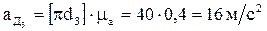А также величины относительных касательных ускорений:

^,

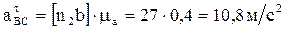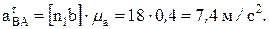
Определяем величины угловых ускорений звеньев

^.

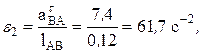
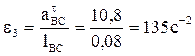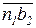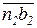Перенося вектора и ускорени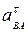й и 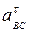, в точку В, находим направление угловых ускорений ( 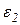направлено против хода часовой стрелки, а 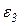– по ходу часовой стрелки).