Пример 2.3

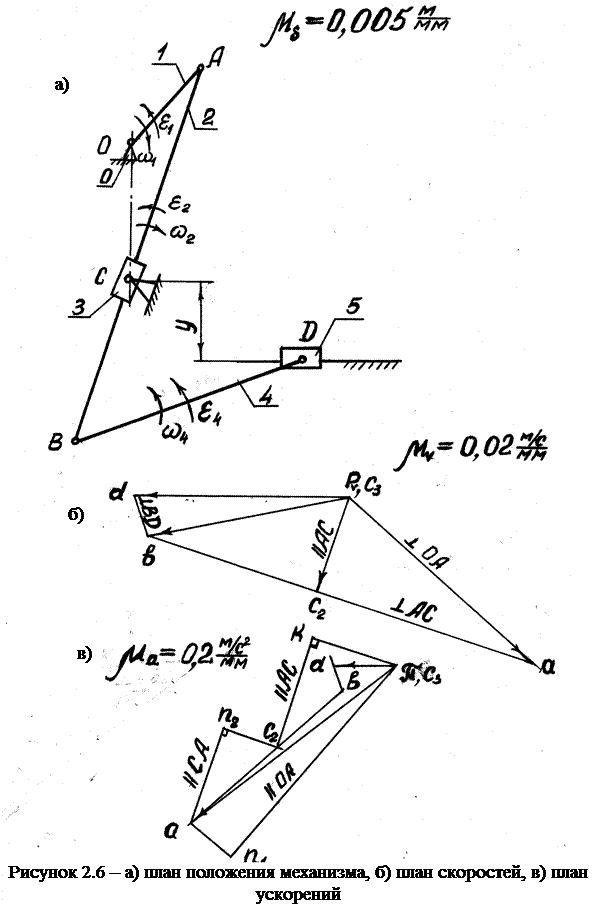
Определить скорость и ускорение ползуна Д механизма, изображенного на рис. (2.6) в положении, когда φ₁ = 45°.

Размеры звеньев механизма заданы:

l_ОА = 0,15 м; l_ОС = 0,2 м; l_AB = 0,575 м; l_АД = 0,35 м; у = 0,11 м. В данном положении механизма w₁= 10с^-1; 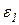= 20с^-2.

Решение:

Выполняем структурный анализ механизма.

Число степеней свободы механизма:

W = 3n–2p5–p4 =3·5–2·7 = 1.

Следовательно, в механизме одно входное звено.

Структурная формула механизма:

I(0,1)→II(2,3)→II(4,5).

Согласно структурной формуле последовательность кинематического анализа следующая:

А→С₀ →С₂ →В→Д₀→Д₅,

где т. А – конец первого звена, т.т. А и С₀ внешние точки диады (2,3);

т. С₂ – внутренняя точка этой диады.

В диаде (4,5) т. В и т. Д₀ – внешние точки диады, т. Д₅ – внутренняя точка.

Строим механизм в заданном положении.

Выбираем масштабный коэффициент длин:

^.

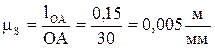Тогда отрезки, изображающие длины звеньев будут

АВ = 115 мм; ОС = 40 мм; ВД = 70 мм; [у] = 22мм.

Построение плана скоростей начинаем с определения скорости конца кривошипа т. А

^.

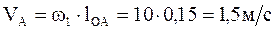Отрезок изображающий V_A, принимаем =75мм. Тогда масштабный коэффициент скоростей

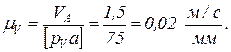
Откладываем 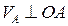в сторону w₁.

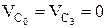т.к. эта точка неподвижна и на плане скоростей будет размещаться в полюсе p_V плана. Для т. С₂ составим систему двух векторных уравнений:

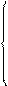
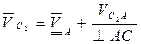(2.9)

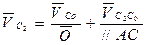
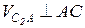т.к. обе точки принадлежат звену 2, имеющему плоскопараллельное движение, 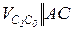т.к. т. С₂ принадлежит кулисе 2, а С₀(С₃) – кулисному камню, а движение кулисы 2 в кулисном камне 3 прямолинейное. Решаем уравнения (2.9) графически. Получим точку «с₂» на плане. V_B находим методом подобия, т.к. на звене 2 известны уже скорости т.т. А и С₂. Точки А, С₂ и В на звене образуют прямую линию, в такой же последовательности эти точки расположатся на плане скоростей. Составим соответствующую пропорцию:

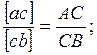
Построенную на плане точку «b» соединяем с полюсом плана скоростей. Этот вектор изображает .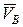

Переходим к определению скоростей в диаде (4,5). 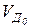=0, т.к. точка Д₀ принадлежит стойке О.

Для точки Д₅ составим два векторных уравнения:

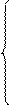
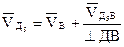(2.10)

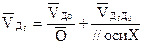
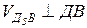, т.к. т. В и т. Д₅ принадлежат звену 4, совершающему плоскопараллельное движение. 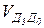// оси X, т.к. точка Д₃ принадлежит ползуну 5, а т. Д₀ – стойке. Ползун относительно стойки движется по прямой X. Решаем систему (2.10), графически получим точку «d₅». План скоростей построен. Из него получаем абсолютные скорости:

^,

^,

^.

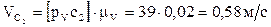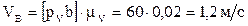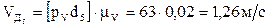Относительные скорости:

^,

^.

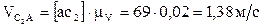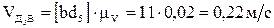Вычисляем модули угловых скоростей звеньев 2 и 4:

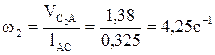
Направление w₂ определяем, перенося вектор 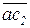в т. С₂ механизма (по часовой стрелке), направление w₄ определяем, перенося вектор 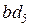в т. Д механизма (против хода часовой стрелки).

В той же последовательности строим план ускорений. Ускорение конца кривошипа состоит из двух составляющих:

^,

^,

^.

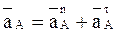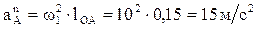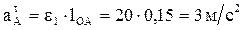Выбираем масштабный коэффициент плана ускорений. Выбираем отрезок 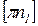=75 мм, изображающий .

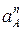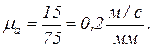
Тогда 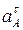изображаем отрезком

^.

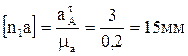Ускорение нормальное т. А 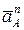// ОА и направлено от т. А к т. О. Ускорение 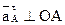и показывается на плане отрезком 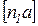отложенным в направлении 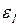. Соединив точку «а» с полюсом плана ускорений получим абсолютное ускорение т. А.

Переходим к структурной группе (2,3). 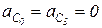, т.к. точка неподвижна. Для внутренней точки данной диады составим систему двух уравнений:

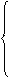
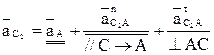(2.11)

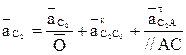
Направления ускорений указаны согласно аналогичным рассуждениям при построении плана скоростей.

В первом уравнении:

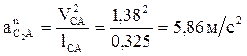
Отрезок, изображающий :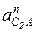

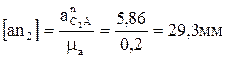
Во втором уравнении системы (2.11)

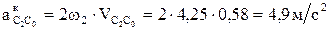
Отрезок, изображающий это ускорение на плане ускорений

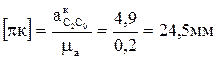
Направление ускорения Кориолиса определяем по правилу Жуковского. Для этого вектор 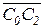поворачиваем на 90° по часовой стрелке (направление w₂). Поэтому 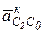будет направлено влево 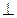АС. Решая графически систему (2.11), получим ускорение т. С₂.

Ускорение т. В находим методом подобия, составив пропорцию:

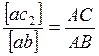
^Откуда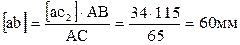

Соединив точку «b» с полюсом плана ускорений получим абсолютное ускорение точки В.

Определяем ускорения в структурной группе (4,5): 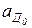=0. Для внутренней точки диады Д₅ составим два векторных уравнения:

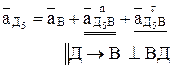(2.12)

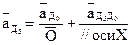
В первом уравнении определяем :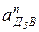

^.

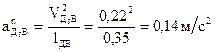На плане ускорений отрезок, изображающий это ускорение будет равен:

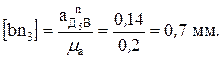
Следовательно, на плане ускорений этот отрезок не показываем. Решаем систему уравнений (2.12) графически. Получим ускорение точки Д₅. План ускорений построен. Из него получаем абсолютные ускорения точек звеньев:

^{, ,}

^{, .}

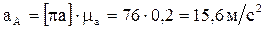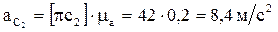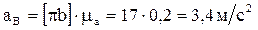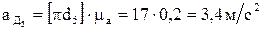Относительные касательные ускорения:

^{, .}

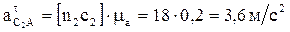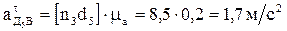Определяем величины угловых ускорений e₂ и e₄ звеньев 2 и 4:

^{, .}

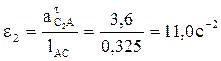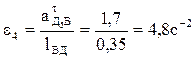Перенося вектор 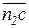ускорения 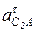в точку С звена 2 и повернув звено в направлении вектора относительно т. А, получим направление e₂ против хода часовой стрелки.

Вектор 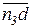ускорения 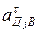перенесем в т. Д звена 4 и повернем звено в направлении этого вектора вокруг полюса В. Получим направление углового ускорения звена 4 (против хода часовой стрелки).