Азн. 11.1. Калі V - лінейная прастора над над Р, а f: V 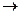 V – лінейнае адлюстраванне, тады f называецца лінейным аператарам, ці эндамарфізмам прасторы V. Мноства эндамарфізмаў прасторы V абазначаецца EndP(V), ці End(V).
V – лінейнае адлюстраванне, тады f называецца лінейным аператарам, ці эндамарфізмам прасторы V. Мноства эндамарфізмаў прасторы V абазначаецца EndP(V), ці End(V).
Азн. 11.2. Няхай V -лінейная прастора над Р, dim V =n, f ÎEnd(V) і базіс V
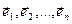 . (1)
. (1)
Абазначым 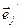 =
= 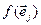 =
= 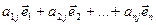 =
= 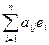 . (2)
. (2)
Матрыца А =(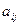 ) сістэмы вектароў
) сістэмы вектароў 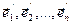 у базісе (1) называецца матрыцай эндамарфізма f у базісе (1).
у базісе (1) называецца матрыцай эндамарфізма f у базісе (1).
Пр. 11. 3. 1) D: 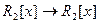 :
: 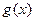
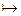
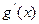
Эндамарфізм D у базісе 1, x, x2 мае матрыцу А = 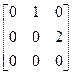
 .
.
2) Эндамарфізм 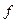 - паварот
- паварот 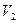 вакол пункта 0 на вугал
вакол пункта 0 на вугал 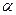 , у базісе
, у базісе 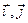 мае матрыцу
мае матрыцу 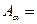
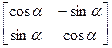
3) Знойдзем матрыцу таго ж эндамарфізма 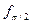 у базісе
у базісе 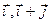 :
:
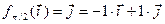 ;
;
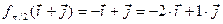 .
.
Такім чынам, эндамарфізм 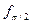 у базісе
у базісе 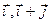 мае матрыцу
мае матрыцу 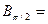
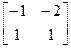 .
.
(Заўважам, што ў базісе 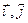 ён мае матрыцу
ён мае матрыцу 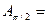
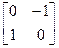 ).
).
Ул-ць 11.4. Калі (1)-базіс лінейнай прасторы, тады кожнаму эндамарфізму адпавядае некаторая матрыца з Mat(n´n,Р). Кожнай матрыцы А ÎMat(n´n,P) адпавядае эндамарфізм f ÎEnd(V), які ў базісе (1) мае матрыцу А.
Доказ. Адпаведнасць эндамарфізму матрыцы эндамарфізму дадзена ў азначэнні 11.2. Няхай дадзена матрыца. Праз 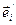 абазначым вектар, каардынатамі якога ў базісе (1) з’яўляецца і -ты слупок матрыцы А. Па тэаоэме 8.4 існуе эндамарфізм f прасторы V такі, што
абазначым вектар, каардынатамі якога ў базісе (1) з’яўляецца і -ты слупок матрыцы А. Па тэаоэме 8.4 існуе эндамарфізм f прасторы V такі, што 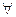 i f (
i f (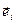 ) =
) = 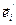 . Відавочна, што f у базісе (1) мае матрыцу А. ■
. Відавочна, што f у базісе (1) мае матрыцу А. ■
Тэарэма 11.5. Няхай (1) – базіс V, f ÎEnd(V) і A -матрыца f у базісе (1). Для аадвольнага вектара 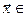 V, калі Х - слупок яго каардынат у базісе (1), тады слупок каардынат Y вектара
V, калі Х - слупок яго каардынат у базісе (1), тады слупок каардынат Y вектара 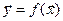 у базісе (1) роўны Y =
у базісе (1) роўны Y = 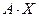 .
.
Доказ. Няхай 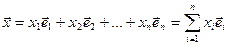 ,
, 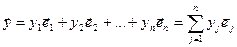 , тады
, тады 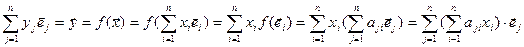 . Паколькі (1) – базіс, атрымоўваем, што
. Паколькі (1) – базіс, атрымоўваем, што 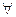 j =
j = 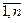

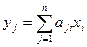 . Застаецца заўважыць, што
. Застаецца заўважыць, што 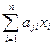 - гэта j -ты элемент слупка, які з’яўляецца здабыткам матрыцы А на слупок Х. Такім чынам даказалі, што Y =
- гэта j -ты элемент слупка, які з’яўляецца здабыткам матрыцы А на слупок Х. Такім чынам даказалі, што Y = 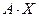 .■
.■
Прыклад 11.6. У прыкладзе 11.3.2 мы разглядалі аператар 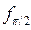 : V2
: V2 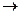 V2. Паспрабуем рознымі шляхамі знайсці
V2. Паспрабуем рознымі шляхамі знайсці 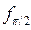 (
(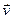 ), дзе
), дзе 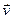 =
= 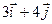 .
.
Рашэнне 1. Паколькі 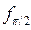 (
(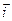 )=
)= 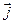 ;
; 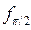 (
(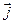 )= -
)= - 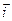 , тады
, тады 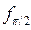 (
(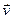 ) =
) = 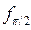 (
(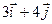 )= =3
)= =3 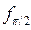 (
(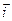 )+4
)+4 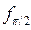 (
(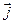 ) =3
) =3 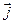 +4(-
+4(- 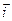 ) =-4
) =-4 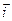 +3
+3 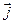 .
.
Рашенне 2. У базісе 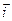 ,
, 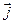 аператар
аператар 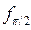 мае матрыцу А =
мае матрыцу А = 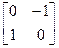 , а вектар
, а вектар 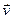 мае слупок каардынат Х =
мае слупок каардынат Х = 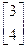 . Згодна з тэарэмай 11.5 вектар
. Згодна з тэарэмай 11.5 вектар 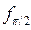 (
(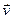 ) у базісе
) у базісе 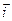 ,
, 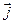 мае слупок каардынат Y=АХ =
мае слупок каардынат Y=АХ = 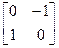 ×
× 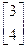 =
= 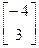 . Гэты адказ адпавядае атрыманаму раней.
. Гэты адказ адпавядае атрыманаму раней.
Паспрабуем яшчэ адказаць на пытанне: якія каардынаты мае вектар 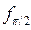 (
(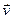 ) у базісе
) у базісе 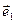 =
= 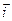 ,
, 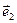 =
= 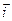 +
+ 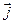 ?
?
Рашэнне 1. Дастаткова знайсці каардынаты вектара -4 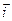 +3
+3 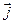 у базісе
у базісе 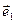 ,
, 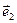 . Гэта можна зрабіць па азначэнню каардынат вектара у базісе:
. Гэта можна зрабіць па азначэнню каардынат вектара у базісе:
-4 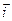 +3
+3 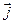 = х
= х 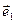 +у
+у 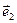 ,
,
-4 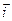 +3
+3 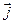 = х
= х 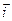 +у(
+у(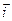 +
+ 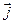 ),-4
),-4 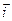 +3
+3 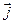 = (х+у)
= (х+у) 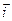 +у
+у 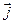 .
.
Паколькі 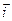 ,
, 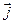 - базіс,
- базіс, 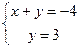 , значыцца,
, значыцца, 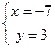 і
і 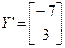 .
.
Рашэнне 2. Матрыца Т пераходу ад базіса 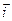 ,
, 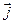 да базіса
да базіса 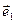 ,
, 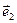 - роўная Т =
- роўная Т = 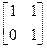 .
.
Па тэарэме 6.8 слупкі каардынат Х і 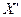 вектара ў базісах
вектара ў базісах 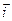 ,
, 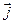 і
і 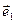 ,
, 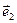 звязаны залежнасцю
звязаны залежнасцю 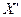 =
= 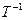 Х.
Х.
Паколькі 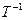 =
= 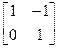 , атрымоўваем:
, атрымоўваем: 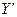 =
= 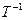 Y =
Y = 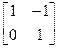 ×
× 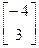 =
= 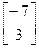 .
.
Рашэнне 3. Як у рашэнні 2, 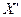 =
= 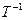 Х =
Х = 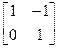 ×
× 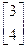 =
= 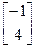 . У прыкладзе 11.3.2 знайшлі, што аператар
. У прыкладзе 11.3.2 знайшлі, што аператар 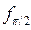 мае ў базісе
мае ў базісе 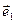 ,
, 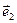 матрыцу В =
матрыцу В = 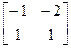 . Тады згодна з тэарэмай 11.5
. Тады згодна з тэарэмай 11.5 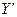 = В
= В 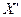 =
= 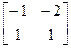 ×
× 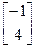 =
= 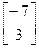 .
.
Лема 11.7. Няхай матрыцы С, D Î Mat(m´n,P) такія, што для адвольнага слупка Х ÎMat (n ´1,P) СХ = DX , (3)
тады С = D.
Доказ. Паколькі Х – адвольная матрыца, разгледзім паступова слупкі Х, у якіх адзін элемент роўны 1, а астатнія- 0.
Калі Х = 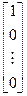 , з роўнасці (3) відавочна атрымоўваецца, што ў матрыцах С і D першыя слупкі роўныя. Калі Х =
, з роўнасці (3) відавочна атрымоўваецца, што ў матрыцах С і D першыя слупкі роўныя. Калі Х = 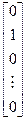 , тады атрымоўваем роўнасць другіх слупкоў матрыц С і D.
, тады атрымоўваем роўнасць другіх слупкоў матрыц С і D.
Такім чынам, атрымаем, што ўсе адпаведныя слупкі матрыц С і D роўныя, з чаго вынікае роўнасць С = D. ■
Тэарэма 11.8. Няхай f – лінейны аператар прасторы V, (1) і
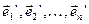 (4)
(4)
базісы прасторы V, Т -матрыца пераходу ад базіса (1) да базіса (4), А і В – матрыцы аператара f у базісах (1) і (4) адпаведна. Тады В = 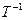 АТ.
АТ.
Доказ. Па тэарэме 11.5, калі Y і 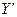 - адпаведна слупкі каардэнат вектара f (
- адпаведна слупкі каардэнат вектара f (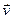 ) у базісах (1) і (4), маем
) у базісах (1) і (4), маем 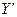 = В
= В 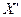 і Y=АХ. Па тэарэме 6.8
і Y=АХ. Па тэарэме 6.8 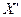 =
= 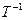 Х і
Х і 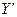 =
= 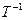 Y.
Y.
Такім чынам, 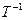 Y=В
Y=В 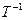 Х, адкуль (
Х, адкуль (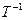 А)Х=(В
А)Х=(В 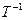 )Х. Паколькі вектар
)Х. Паколькі вектар 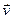 , і значыцца, слупок Х - адвольны, па леме 11.7 атрымоўваем, што
, і значыцца, слупок Х - адвольны, па леме 11.7 атрымоўваем, што 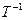 А= В
А= В 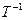 , і В =
, і В = 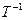 АТ. ■
АТ. ■
Азн. 11.9. Квадратныя матрыцы A і B вымернасці n ´ n называюцца спалучанымі, калі існуе матрыца S вымернасці n ´ n, такая што A= 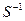 BS.
BS.
 2015-07-14
2015-07-14 288
288







