Прыклад12.15

12.15.1. ε = V₂ – гэта звыклы вугал паміж вектарамі з курса геаметрыі.

12.15.2. ε = C[a,b]– з прыкладаў 12.2.2 і 12.6.2.

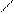
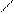cos(f, g)= .

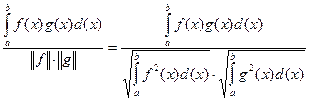Няроўнасць Кашы-Бунякоўскага мае выгляд:

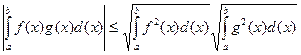
12.15.3. У R ⁿ скалярны здабытак можа быць зададзены наступным чынам:

калі 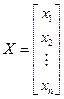, Y = 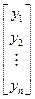. Азначым (X, Y) = x₁y₁₊ x₂y_2+…+ x_ny_n= 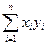, у гэтым выпадку Эўклідава прастора абазначаецца R ⁿ ці ε ⁿ .

Па 12.5 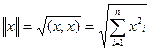. З 12.10 вынікае, што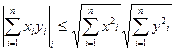

Вынік 12.16. (Тэарэма косінусаў у эўклідавай прасторы)

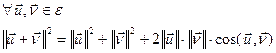
Доказ. . ■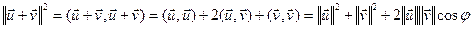

Вынік 12.17. (Няроўнасць трохвугольніка ў эўклідавай прасторы)

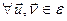
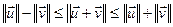
Доказ. Дакажам правую частку няроўнасці:

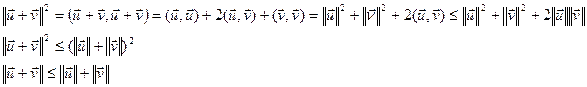
Дакажам левую частку няроўнасці: ; ;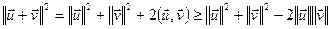

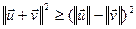Пры доказе два разы выкарысталі няроўнасць Кашы-Бунякоўскага.■