Прыклад 12.2.
1. V2 са скалярным здабыткам, які вывучаўся ў курсе геаметрыі: калі  =
= 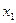
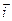 +
+ 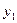
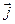 ,
,  =
= 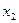
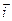 +
+ 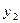
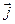 (
( ;
;  )=
)= 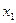
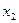 +
+ 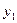
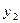 з’яўляецца эўклідавай прасторай.
з’яўляецца эўклідавай прасторай.
2. С [a;b]- мноства непарыўных на [a;b] функцый.
Калі f, g Î С [a;b], азначым (f, g)= 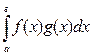 . Праверце, што на С [a;b] зададзены скалярны здабытак, такім чынам, С [a;b]- эўклідава прастора.
. Праверце, што на С [a;b] зададзены скалярны здабытак, такім чынам, С [a;b]- эўклідава прастора.
Ул-ць 12.3. У адвольнай эўклідавай прасторы ε:
1) 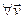 Î ε (
Î ε ( ;
; 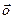 )=(
)=(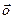 ;
;  )=
)= 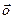 ;
;
2) 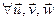 Î ε (
Î ε (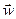 ;
;  +
+  )=(
)=(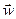 ;
;  )+(
)+(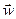 ;
;  );
);
3) 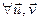 Î ε
Î ε 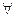
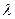 ÎR (
ÎR ( ;
; 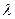
 )=
)= 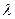 (
( ;
;  );
);
4) 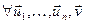 Î ε,
Î ε, 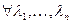 ÎR (
ÎR (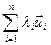 ;
;  )=
)= 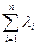 (
(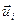 ;
;  );
);
5) 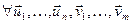 Î ε
Î ε 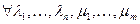 ÎR (
ÎR (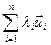 ;
; 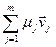 )=
)= 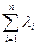
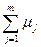 (
(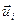 ;
; 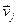 ).
).
Доказ.
1) ( ;
; 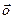 )=(
)=( ;0
;0  )=0(
)=0( ;
;  )=0.
)=0.
2) (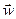 ;
;  +
+  )=(
)=( +
+  ;
; 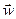 )=(
)=( ;
; 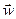 )+(
)+( ;
; 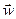 )=(
)=(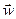 ;
;  )+(
)+(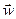 ;
;  ).
).
3) ( ;
; 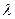
 )=(
)=(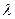
 ;
;  )=
)= 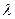 (
( ;
;  )=
)= 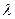 (
( ;
;  ).
).
4) ММІ па п.
п =1 (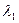
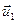 ;
;  )=
)= 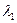 (
(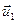 ;
;  ) па 12.1.3.
) па 12.1.3.
п =2 (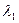
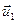 +
+ 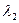
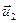 ;
;  )=(
)=(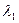
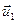 ;
;  )+(
)+(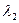
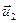 ;
;  )=
)= 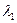 (
(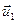 ;
;  )+
)+ 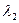 (
(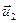 ;
;  ).
).
Калі праўдзіцца для п, разгледзім п +1. (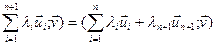 = =
= = 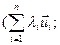
 )+(
)+(
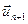 ;
;  ) =
) = 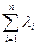 (
(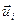 ;
;  )+
)+  (
(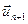 ;
;  ) =
) = 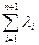 (
(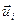 ;
;  ).
).
5) (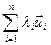 ;
; 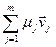 )=
)= 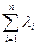 (
(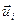 ;
; 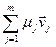 )=
)= 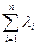 (
(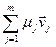 ;
; 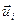 )=
)= 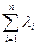
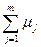 (
(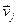 ;
; 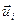 )=
)=
= 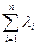
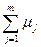 (
(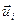 ;
; 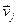 ).■
).■
Ул-ць 12.4. Няхай V - эўклідава прастора са скалярным здабыткам (·; ·), U - падпрастора ў V. Тады U са скалярным здабыткам (·; ·): U ´ U 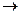 R з’яўляецца эўклідавай прасторай.
R з’яўляецца эўклідавай прасторай.
Доказ. Відавочна з азначэння 12.1 ■.
Азн. 12.5.Даўжынёй (нормай) вектара  Î ε называецца рэчаісны лік
Î ε называецца рэчаісны лік 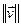 =
= 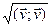 .
.
З 12.1.4 і 12.3.1 вынікае, што 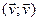
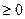 і
і 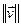 азначана карэктна.
азначана карэктна.
Прыклад 12.6.
12.6.1. У 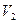
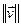 адпавядае геаметрычнаму азначэнню даўжыні вектара.
адпавядае геаметрычнаму азначэнню даўжыні вектара.
12.6.2. У С [a;b] 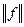 =
= 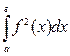 .
.
Ул-ць 12.7. У эўклідавай прасторы ε:
1) 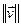 = 0 тады і толькі тады, калі
= 0 тады і толькі тады, калі  =
= 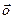 ;
;
2) 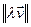 =
= 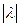
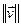 .
.
Доказ.
1) Калі  =
= 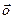 , тады
, тады 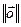 =
= 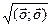 =
= 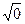 =0. Калі
=0. Калі 
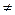
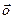 , тады
, тады 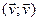 >0, адкуль
>0, адкуль 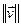 =
= 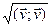 >0.
>0.
2) 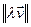 =
= 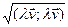 =
= 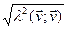 =
= 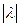
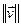 .■
.■
Азн. 12.8. Вектар  Î ε называецца нармаванным, калі
Î ε называецца нармаванным, калі 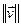 =1.
=1.
Ул-ць 12.9. Калі 
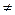
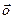 , тады вектар
, тады вектар 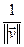
 - нармаваны.
- нармаваны.
Доказ. 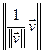 =
= 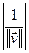
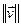 =
= 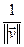
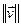 =1.■
=1.■
Уласцівасць 12.10. (Няроўнасць Кашы-Бунякоўскага)
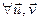 Î ε
Î ε 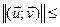
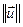
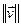 (1)
(1)
Роўнасць у (1) мае мейсца тады і толькі тады, калі  і
і  - калініярныя, гэта значыць
- калініярныя, гэта значыць 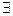 kÎR такі, што
kÎR такі, што  =k
=k  (ці
(ці  = k
= k  ).
).
Доказ. Калі  =
= 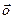 , тады (1) праўдзіцца па 12.3.1 і
, тады (1) праўдзіцца па 12.3.1 і  =0
=0  .
.
Калі 
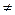
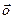 па 12.1.4 і 12.3.1 (
па 12.1.4 і 12.3.1 (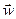 ;
; 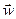 )
) 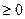 , значыцца
, значыцца 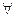
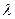
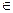 R (
R ( -
- 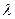
 ;
;  -
- 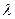
 )
) 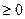 , (2) значыцца,
, (2) значыцца, 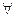
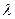
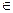 R
R 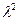
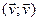 -2
-2 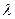
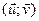 +
+ 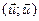
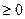 . (3)
. (3)
Паколькі 
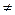
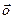 , квадратны трохсклад у левай часцы (3) дадатны пры усіх
, квадратны трохсклад у левай часцы (3) дадатны пры усіх 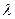
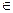 R. Гэта магчыма тады і толькі тады, калі
R. Гэта магчыма тады і толькі тады, калі 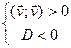 , дзе D– дыскрымінант квадратнага трохскладу.
, дзе D– дыскрымінант квадратнага трохскладу.
Паколькі 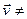
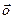 , першая няроўнасць сістэмы выконваецца.
, першая няроўнасць сістэмы выконваецца.
D<0 значыцца 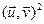 ≤
≤ 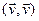 ×
× 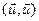 што эквівалентна
што эквівалентна 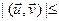 ||
||  ||×||
||×||  || (4)
|| (4)
Калі 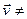
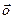 , роўнасць у (1) мае месца тады і толькі тады, калі мае месца роўнасцьу (4), што эквівалентна таму што няроўнасць (3) а, значыцца і няроўнасць (2), становяцца роўнасцямі, а гэта магчыма толькі калі: (
, роўнасць у (1) мае месца тады і толькі тады, калі мае месца роўнасцьу (4), што эквівалентна таму што няроўнасць (3) а, значыцца і няроўнасць (2), становяцца роўнасцямі, а гэта магчыма толькі калі: ( -λ
-λ  ,
,  -λ
-λ  )=0.
)=0.
З гэтага па 12.7.1 атрымоўваем, што:  -λ
-λ  =0 і
=0 і  =λ
=λ  .
.
Калі  =
= 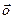 , тады ў (1) мае месца роўнасць і
, тады ў (1) мае месца роўнасць і  =0
=0  .■
.■
Вынік 12.11. Калі  ,
,  належаць ε \ {
належаць ε \ { 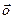 , } тады -1 ≤
, } тады -1 ≤ 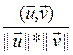 ≤ 1.
≤ 1.
Доказ. З 12.11 вынікае, што - ||  ||×||
||×||  ||
||  (
( ,
,  )
)  ||
||  ||×||
||×||  ||, значыцца,-1 ≤
||, значыцца,-1 ≤ 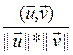 ≤ 1.■
≤ 1.■
Ул-ць 12.12. Калі  ,
,  належаць ε \ {
належаць ε \ { 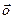 }, тады існуе адзіны φ з прамежка [0,
}, тады існуе адзіны φ з прамежка [0, 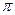 ] такі, што: cosφ=
] такі, што: cosφ= 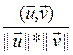 .
.
Доказ. Доказ вынікае з 12.11 і з таго што на [0, 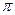 ]функцыя cos(x) прыймае значэнні ад -1 да 1 па аднаму разу.■
]функцыя cos(x) прыймае значэнні ад -1 да 1 па аднаму разу.■
Азн. 12.13. Калі  ,
,  належаць ε \ {
належаць ε \ { 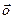 }, тады вуглом паміж вектарамі
}, тады вуглом паміж вектарамі  і
і  называюць вугал φ з прамежка [0,
называюць вугал φ з прамежка [0, 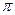 ] такі што
] такі што

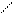 cos φ=
cos φ= 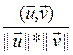 , φ = (
, φ = ( ,
,  ).
).
З 12.12 вынікае карэктнасць 12.13.
Вынік 12.14. 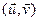 =||
=||  ||×||
||×||  ||× cos φ.
||× cos φ.
Доказ. Відавочна з 12.13. ■
 2015-07-14
2015-07-14 313
313








