Квадратычныя формы
Азначэнне 19.1.Квадратычнай формай ад літар (зменных) 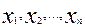 называюцца
называюцца
F (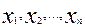 ) =
) = 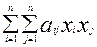 , (1)
, (1)
дзе 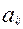
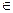 R.
R.
Калі ў (1) прысутнічаюць складнікі 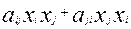 , тады іх суму магчыма запісаць ў выглядзе
, тады іх суму магчыма запісаць ў выглядзе 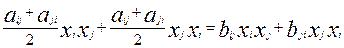 ,
,
прычым, відавочна, 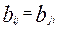 .Такім чынам, у далейшым будзем лічыць, што
.Такім чынам, у далейшым будзем лічыць, што 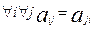 .
.
Уласцівасць 19.2. Калі атаесаміць рэчаісны лік 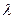 і матрыцу
і матрыцу 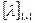 тады
тады
F (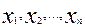 ) =
) = 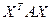 , (2)
, (2)
дзе A = (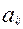 )
) 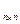 - сіметрычная матрыца каэфіцыентаў квадратычнай формы, а
- сіметрычная матрыца каэфіцыентаў квадратычнай формы, а 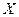 – слупок невядомых (зменных).
– слупок невядомых (зменных).
Доказ: Дастаткова знайсці здабытак у (2) і атрымаць (1). ■
Прыклад 19.3.
19.3.1. Квадратычная форма 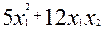 мае матрыцу A =
мае матрыцу A = 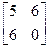 .
.
19.3.2. Квадратычная форма 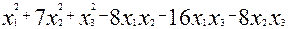
 мае матрыцу
мае матрыцу
A = 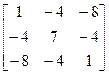 .
.
Азначэнне 19.4. Няхай зменныя 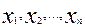 лінейна выяўляюцца праз зменныя
лінейна выяўляюцца праз зменныя 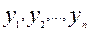 наступным чынам:
наступным чынам: 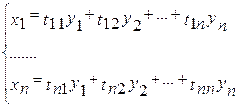 (3)
(3)
Калі замест 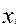 у (1) падставім іх выяўленне праз
у (1) падставім іх выяўленне праз 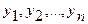 па формулам (3), тады атрымаем квадратычную форму F (
па формулам (3), тады атрымаем квадратычную форму F ( 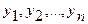 ). Пры гэтым будзем казаць, што новая квадратычная форма атрымана з (1) з дапамогай замены (3).
). Пры гэтым будзем казаць, што новая квадратычная форма атрымана з (1) з дапамогай замены (3).
У выніку замены атрымаем квадратычную форму адносна зменных 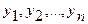 так як пасля раскрыцця дужак атрымаем складнікі другой ступені адносна
так як пасля раскрыцця дужак атрымаем складнікі другой ступені адносна 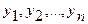 .
.
Азначэнне 19.5. Матрыца 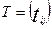 называецца матрыцай замены (3).
называецца матрыцай замены (3).
Уласцівасць 19.6. Калі квадратычная форма F1( 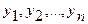 ) атрымана з квадратычнай формы (1) з дапамогай замены (3) з матрыцай Т, тады новая квадратычная форма мае матрыцу
) атрымана з квадратычнай формы (1) з дапамогай замены (3) з матрыцай Т, тады новая квадратычная форма мае матрыцу 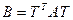 (4)
(4)
Доказ: Няхай X і Y – слупкі зменных 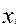 і
і 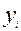 . Відавочна, што згодна з (3)
. Відавочна, што згодна з (3) 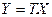 . Тады па 19.2, калі В – матрыца квадратычнай формы F1, тады F1 =
. Тады па 19.2, калі В – матрыца квадратычнай формы F1, тады F1 = 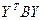 . Але, з (2) вынікае, што F1(
. Але, з (2) вынікае, што F1( 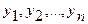 ) =
) = 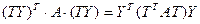 . Для таго каб даказаць, што
. Для таго каб даказаць, што 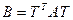 застаецца паказаць, што матрыца
застаецца паказаць, што матрыца 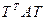 – сіметрычная. На самой справе,
– сіметрычная. На самой справе, 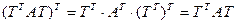 (мы выкарысталі тое, што А – сіметрычная матрыца).■
(мы выкарысталі тое, што А – сіметрычная матрыца).■
Прыклад 19.7. Разгледзім квадратычную форму F(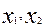 ) =
) = 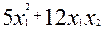 . Выдзелім у ёй поўны квадрат па зменнай
. Выдзелім у ёй поўны квадрат па зменнай 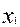 :
: 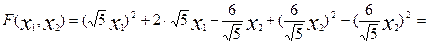
= 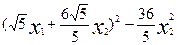 . (5)
. (5)
Відавочна, што калі ў квадратычнай форме F(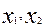 ) абазначым
) абазначым 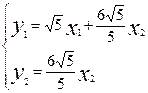 , (6) тады (5) будзе роўная
, (6) тады (5) будзе роўная 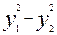 . Выявім з (6)
. Выявім з (6) 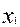 і
і 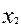 праз
праз 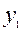 і
і 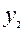 :
: 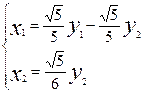 .(7)
.(7)
Формулы (7) з’яўляюцца формуламі замены, у выніку якой квадратычная форма 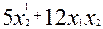 прыводзіцца да выгляду
прыводзіцца да выгляду 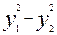 .
.
Нескладана убачыць, што 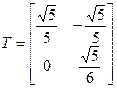 – матрыца замены (7).
– матрыца замены (7).
У 19.3.1. знайшлі, што квадратычная форма 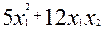 мае матрыцу
мае матрыцу 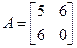 . Квадратычная форма
. Квадратычная форма 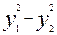 мае матрыцу
мае матрыцу 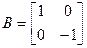 . Нескладана праверыць, што
. Нескладана праверыць, што 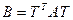 адпавядае 19.6.
адпавядае 19.6.
Азначэнне 19.8. Кажуць, што квадратычная форма мае кананічны выгляд, калі яе матрыца – дыяганальная.
У прыкладзе 19.7 мы знайшлі замену (7), з дапамогай якой квадратычную форму з прыклада 19.3.1. прывялі да кананічнага выгляду 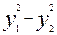 .
.
Відавочна, што квадратычныя формы, якія маюць кананічны выгляд – найбольш простыя і зручныя да даследавання. Далей у гэтым параграфе мы разгледзім пытанне аб адшуканні замены, з дапамогай якой дадзеная квадратычная форма прыводзіцца да кананічнага выгляду.
Тэарэма 19.9. Для кожнай квадратычнай формы існуе замена, якая прыводзіць форму да кананічнага выгляду, прычым, існуе неабходная замена, матрыца T якой - артаганальная.
Доказ: Няхай дадзена квадратычная форма (1) з матрыцай А. Разгледзім эўклідаву прастору  і фіксуем у ёй некаторы ортаўнармаваны базіс. Па ўласцівасці 11.4 існуе аператар f прасторы
і фіксуем у ёй некаторы ортаўнармаваны базіс. Па ўласцівасці 11.4 існуе аператар f прасторы  , які ў дадзеным базісе мае матрыцу А. Так як матрыца А – сіметрычная, па 18.4 аператар f – самаспалучаны. Па тэарэме 18.8 існуе ортаўнармаваны базіс з уласных вектараў аператара f, у якім матрыца В аператара – дыяганальная. Калі Т – матрыца пераходу ад старога базіса да новага, тады Т – артаганальная матрыца (абодва базіса – ортаўнармаваныя і застаецца выкарыстаць 15.4 і 15.8), значыцца
, які ў дадзеным базісе мае матрыцу А. Так як матрыца А – сіметрычная, па 18.4 аператар f – самаспалучаны. Па тэарэме 18.8 існуе ортаўнармаваны базіс з уласных вектараў аператара f, у якім матрыца В аператара – дыяганальная. Калі Т – матрыца пераходу ад старога базіса да новага, тады Т – артаганальная матрыца (абодва базіса – ортаўнармаваныя і застаецца выкарыстаць 15.4 і 15.8), значыцца 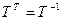 .
.
Тады па тэарэме 11.8 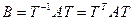 .
.
Такім чынам, атрымалі, што калі ў квадратычнай форме (1) зрабіць замену з артаганальнай матрыцай замены Т, тады атрымаем квадратычную форму, якая мае дыяганальную матрыцу В, значыцца, з’яўляецца кананічнай.■
 2015-07-14
2015-07-14 330
330







