Прыклад 19.10

19.10.1. Разгледзім квадратычную форму з прыкладу 19.3.1.

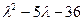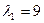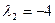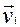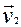Матрыца А гэтай квадратычнай формы мае характэрыстычны паліном і уласныя значэнні і . Гэтыя уласныя значэнні адпавядаюць вектарам і з 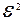, якія маюць слупкі каардынат: 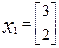і .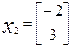

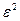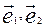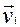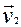Калі мы будзем, як у доказе 19.9, разглядаць лінейны аператар f прасторы , які ў ортаўнармаваным базісе мае матрыцу А, тады і – уласныя вектары самаспалучанага аператара f, якім адпавядаюць няроўныя ўласныя значэнні, значыцца, яны артаганальныя. (У гэтым нескладана ўпэўніцца, калі памятаць, што дадзены базіс – ортаўнармаваны: ).

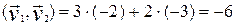Пранармуем вектары 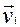і 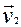і атрымаем вектары 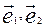, якія маюць слупкі каардынат адпаведна:

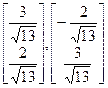, з’яўляюцца ўласнымі вектарамі аператара f і ўтвараюць ортаўнармаваны базіс у 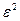. З доказу тэарэмы 19.9 вынікае, што калі ў квадратычнай форме 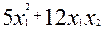зробім замену 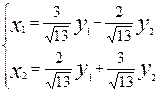з матрыцай 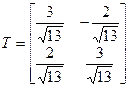, якая ортаганальная (праверце, што 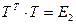), тады атрымаецца квадратычная форма , якая мае кананічны выгляд, так як яе матрыца B = 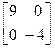- дыяганальная.

(Карыстна праверыць, што ў поўнай адпаведнасці з тэорыяй B = ).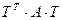

19.10.2. Разгледзім квадратычную форму з прыкладу 19.3.2. Як было паказана ў прыкладзе 17.11.4, матрыца А гэтай формы мае уласныя значэнні 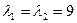(кратнасці 2) і 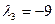, якім адпавядаюць уласныя вектары 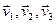са слупкамі каардынат, напрыклад, = , , .

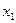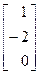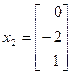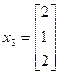Як і раней, так як з аднаго боку вектары 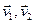і, з другога боку 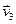адпавядаюць розныя уласныя значэнні, (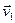, 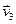)=()=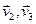0. Але, (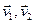) 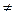0. Выкарыстаем артаганалізацыйны працэс каб пабудаваць ортаўнармаваны базіс 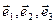з уласных вектароў аператара f, (які ў ортаўнармаваным базісе эўклідавай прасторы 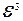мае матрыцу А). Вектары 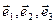у ортаўнармаваным базісе маюць слупкі каардынат , , .

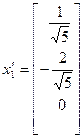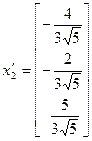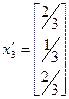Матрыца пераходу да базіса 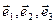Т= 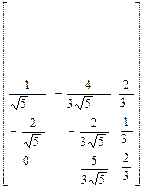- артаганальная.

Такім чынам, калі зрабіць замену

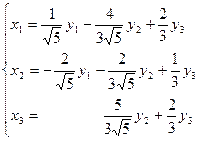, квадратычная форма 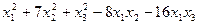прывядзецца да кананічнага выгляду .

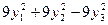Заўвагі 19.11. З прыкладаў 19.7 і 19.10.1 можна заўважыць:

1) Квадратычную форму магчыма прывесці да кананічнага выгляду рознымі заменамі і гэтыя кананічныя выгляды адрозніваюцца адзін ад аднаго.

2) Калі ў 19.10.1 зрабіць замену 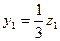, , 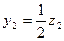тады атрымаем форму 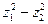, якая нагадвае адказ у 19.7.

3) Калі мы маем квадратычную форму 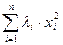у кананічным выглядзе, падобна таму, як гэта зрабілі ў 19.11.2, яе магчыма прывесці да выгляду 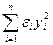, дзе .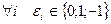

Азначэнне19.12. Калі квадратычная форма мае выгляд

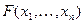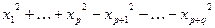= (8)

тады кажуць, што яна прыведзена да сумы квадратаў.

Лема 19.13. Няхай А - матрыца квадратычнай формы 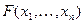. Разгледзім эўклідаву прастору 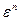і які-небудзь яе ортаўнармаваны базіс. Тады матрыцы А адпавядае самаспалучаны аператар 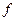, а кожнаму слупку зменных Х= 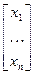адпавядае вектар 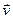, які мае гэты слупок каардынат у гэтым базісе. Тады =(, ()).

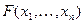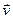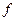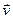Доказ. Так як вектары 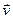, 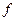(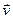) у ортаўнармаваным базісе маюць слупкі каардынат Х і АХ, маем: (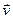, 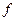(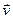))= 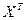АХ= .■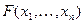

Тэарэма 19.14.(закон інерцыі квадратычных форм). Адвольная квадратычная форма прыводзіцца да сумы каардынат адзіным чынам.

Доказ. Ад процілеглага. Няхай квадратычная форма прыводзіцца да выгляду (8) і да выгляду 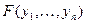= 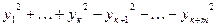(9)

Няхай 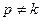. Без страты агульнасці можам лічыць, што p>k. Заўважым, што матрыцы квадратычнай формы можам разглядаць як матрыцы лінейных аператараў f і g у некаторым базісе 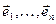прасторы 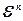. Разгледзім у 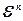падпрасторы V ₁ = 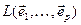і V ₂ = 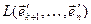. Так як сума вымернасці гэтых падпрастораў роўная р+(п-к)=п+(р-к)>п, значыцца перасячэнне гэтых падпрастораў не роўнае 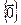(інакш бы атрымалі, што базісы V ₁ і V ₂ разам утрымліваюць больш лінейна незалежных вектараў, чым вымернасць прасторы). 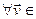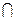Возьмем (V₁ V₂) .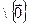

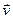
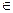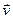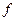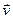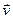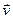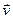
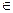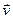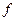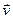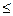Так як V ₁ і (, ())=(, )>0. Так як V ₂, значыцца (, g ()) 0.

Атрымалі супярэчнасць. Выпадак q 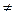m разглядаецца аналагічна.

Сэнс тэрэмы 19.14 у тым, што у адрозненні ад кананічнага выгляду, які азначаны не адзіным чынам, як паказалі ў 19.14, прывядзенне да сумы квадратаў - адзінае.■

На прыканцы прывядзем без доказу тое, што яшчэ датычыцца квадратычных форм.

Азначэнне 19.15. Квадратычная форма 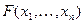называецца дадатна азначанай, калі з таго, што хаця б адзін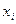 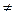0, вынікае, што 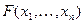>0.

Квадратычная форма 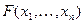называецца адмоўна азначанай, калі з таго, што хаця б адзін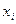 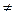0, вынікае, што 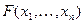<0.

Азн.19.16. Калі А – сіметрычная матрыца, яе вуглавым мінорам парадка k называецца мінор D _k, які ўтвараюць элементы, якія стаяць у яе першых k радках і першых k слупках.