2015-07-14
541
«Дифференциальное исчисление функции одной переменной»
Контрольная работа №1 содержит две группы заданий: в первой группе - три примера на проверку техники дифференцирования явной функции или функции, заданной параметрическим способом. Во второй группе − два задания: одно на геометрические приложения производной, другое на вычисление предела с помощью правила Лопиталя-Бернулли.
При решении задач на вычисление производной функции одной переменной нужно использовать таблицу производных основных элементарных функций, общие правила дифференцирования, правила дифференцирования сложной функции и функции, заданной параметрически, а также логарифмическую производную. Ниже приведены все эти правила.
Общие правила дифференцирования:
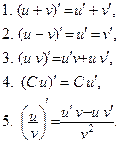
Правило дифференцирования сложной функции функции:
6. 
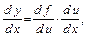если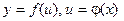 
.
При дифференцировании произведения или частного нескольких функций, а также сложно-степенной функции целесообразно использовать логарифмическую производную: если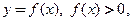 
то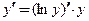 
. Этот прием называют предварительным логарифмированием.
Правило дифференцирования параметрически заданной функции:
7. 
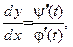или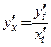 
, если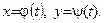 
Уравнения касательной и нормали к графику явной функции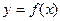 
в точке 
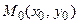, где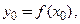 
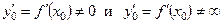, имеют вид:
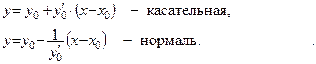
Если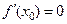 
, то 
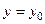− уравнение касательной, 
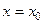− уравнение нормали.
Если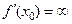 
, то 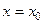− уравнение касательной, 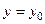− уравнение нормали.
Уравнения касательной и нормали к графику функции, заданной параметрически уравнениями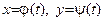 
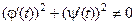) в точке 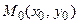, где y 0 = y (t 0 ), x 0 = j (t 0 ), 
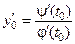, имеют вид:
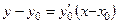− касательная,
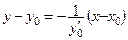− нормаль.
Если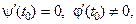 
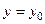то − уравнение касательной, 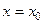− уравнение нормали.
Если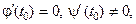 
то 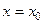− уравнение касательной, 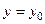− уравнение нормали.
Угловой коэффициент касательной k равен значению производной заданной функции в точке проведения касательной и, как угловой коэффициент прямой, равен тангенсу угла, образованного касательной прямой с положительным направлением оси Ох: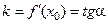 
, где a − угол с Ох.
При вычислении пределов функций, связанных с раскрытием неопределенностей вида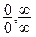 
, можно использовать правила Лопиталя-Бернулли: 
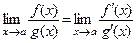, если существует предел 
.
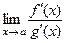При раскрытии неопределенностей вида 0×¥, ¥¤¥, ¥0, 00, 1¥ следует преобразовать исходную функцию с таким расчетом, чтобы далее можно было использовать правила Лопиталя. При вычислении предела сложно-степенной функции, связанного с раскрытием неопределенности одного из трех последних перечисленных выше видов, можно применять предварительное логарифмирование. Ниже приведены: методика выполнения контрольной работы, типовой вариант и его решение.
