При выполнении заданий 1−3 следует:
1) определить способ задания функции − явный или параметрический;
2) в случае явного задания выбрать подходящие правила дифференцирования, определить последовательность их применения и реализовать их;
3) в случае параметрического задания функции воспользоваться правилом 7 параметрического дифференцирования и правилами 1-6 при нахождении производных 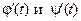 .
.
В задаче 4 следует:
1) определить способ задания функции − явный или параметрический;
2) заполнить таблицу 1, для чего подставить из условий задачи или найти обе координаты 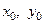 точки
точки 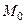 (и
(и 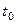 ) и вычислить производную
) и вычислить производную 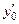 :
:
○ для явной функции 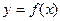 производная
производная 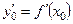 ;
;
○ для функции, заданной параметрическими уравнениями 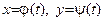 , найти производную
, найти производную 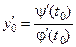 ;
;
3) по значению 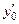 выбрать подходящий частный случай − один из трех: 1)
выбрать подходящий частный случай − один из трех: 1) 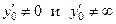 , 2)
, 2) 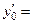 0; 3)
0; 3) 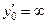 ) и составить уравнение касательной (или уравнение нормали).
) и составить уравнение касательной (или уравнение нормали).
В задаче 5 следует:
1) подставить предельное значение аргумента и определить вид неопределенности;
2) если неопределенность имеет вид 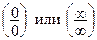 , то применить правило Лопиталя непосредственно. Если получается снова неопределенность вида
, то применить правило Лопиталя непосредственно. Если получается снова неопределенность вида 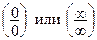 , то повторно применить правило Лопиталя. Если в ходе применения правила Лопиталя получается выражение, не имеющее никакого предела, то следует использовать иной способ решения задачи − тождественные преобразования, эквивалентные функции, замечательные пределы или сочетание приемов;
, то повторно применить правило Лопиталя. Если в ходе применения правила Лопиталя получается выражение, не имеющее никакого предела, то следует использовать иной способ решения задачи − тождественные преобразования, эквивалентные функции, замечательные пределы или сочетание приемов;
3) если получена неопределенность, отличная от случая в п.2, то функцию надо преобразовать так, чтобы получилась неопределенность вида 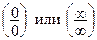 и далее действовать согласно п.2.
и далее действовать согласно п.2.
Типовой вариант
Найдите производные функций:
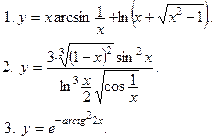
4. Напишите уравнение нормали к кривой х= 3sin t, y = 3cos 3t, в точке, где t0= p/3 .
5. Найдите предел 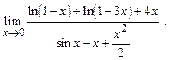
Решение типового варианта
1.a). Применяя последовательно правила дифференцирования, получим:
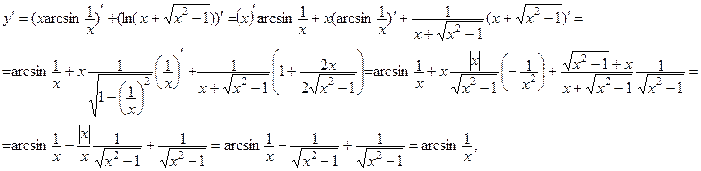
так как в ОДЗ заданной функции 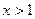 и, следовательно, ½ х ½= х.
и, следовательно, ½ х ½= х.
1.b). При решении этого примера заданную функцию предварительно формально прологарифмируем:
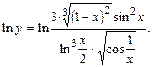
Используем свойства логарифма и упростим выражение в правой части последнего равенства: 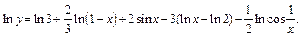
Дифференцируя последнее равенство по х, получим:
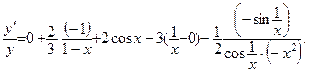
Разрешая последнее равенство относительно производной 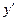 , проходим к следующему результату:
, проходим к следующему результату:
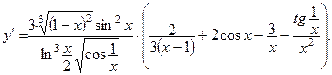
1.c) Применим правило дифференцирования сложной функции. 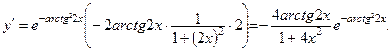
2. Чтобы написать уравнение нормали, нужно найти координаты точки (х 0, у 0) графика функции, через которую проходит нормаль. 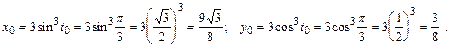
Угловой коэффициент k нормали равен: 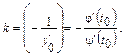
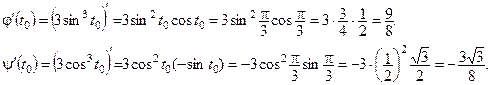
Угловой коэффициент нормали равен 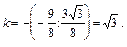 Уравнение нормали имеет вид:
Уравнение нормали имеет вид: 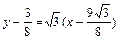 или
или 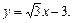
3. Вычисление заданного предела связано с раскрытием неопределенности вида 0/0. Так как функции, образующие частное, дифференцируемы в проколотой окрестности нуля, то в соответствием с правилом Лопиталя получаем: 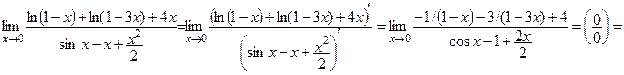
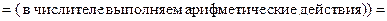
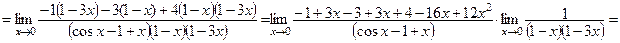
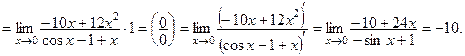
ЛИТЕРАТУРА
1. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. Москва, Наука: 1988.
 2015-07-14
2015-07-14 166
166







