Практическая работа № 15.
Цель работы. Проверить знания и умения учащихся в нахождении производных неявной функции, функции, заданной параметрически, в нахождении производных логарифмическим дифференцированием.
- Производная неявной функции.
Если функции 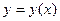 задана уравнением, не разрешенным относительно
задана уравнением, не разрешенным относительно 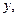
то для нахождения производной 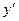 надо продифференцировать по
надо продифференцировать по 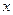 обе части этого уравнения, учитывая, что
обе части этого уравнения, учитывая, что 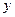 есть функция по
есть функция по 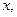 и затем разрешить полученное уравнение относительно
и затем разрешить полученное уравнение относительно 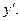 Чтобы найти
Чтобы найти 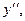 надо уравнение продифференцировать дважды по
надо уравнение продифференцировать дважды по 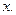
Пример 1. Найти вторую производную 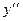 от функции
от функции 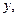 заданной неявно уравнением
заданной неявно уравнением 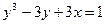
Решение.
Дифференцируя по 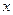 обе части данного равенства и считая при этом
обе части данного равенства и считая при этом 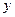 функцией по
функцией по 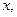 находим
находим
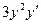
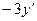
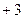
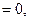
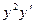
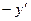
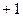
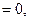
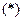
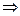
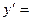
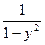
Равенство (*) снова продифференцируем по 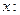
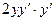
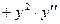
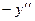
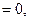
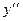
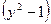
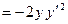
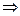
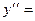
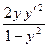
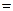
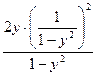
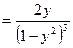
Пример 2. Найти значение 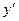 в точке
в точке 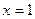 для функции
для функции 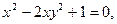
заданной неявно, если 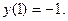
Решение. 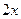
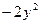
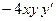
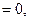 ;
; 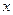
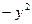
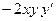
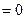
Подставим 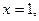
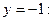
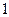
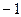
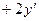
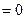
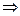
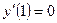
Пример 3. Найти производную функции 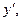 если
если 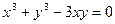
Решение. 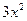
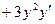
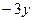
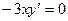
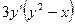
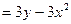 ;
; 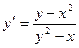
Пример 4. Найти производную функции 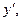 если
если 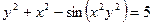
Решение.
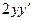
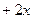
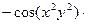
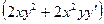
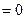
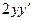
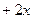
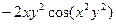
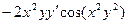
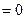
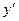
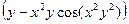
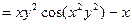
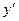
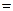
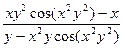
Пример 5. Найти производную функции 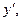 если
если 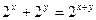
Решение.
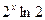
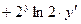
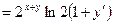 ;
; 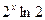
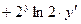
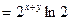
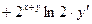
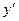
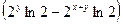
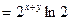
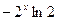 ;
; 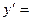
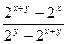
Пример 6. Найти 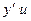
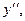 если
если 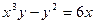
Решение.
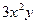
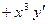
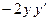
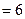
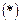 ;
; 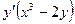
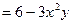 ;
; 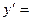
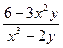
Продифференцируем обе части равенства 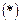 , получим
, получим
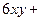
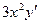
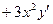
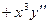
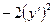
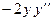
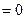
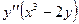
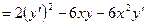
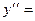
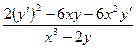
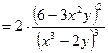
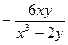
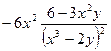
- Логарифмическое дифференцирование.
Логарифмическая производная функции f(x)>0 есть производная от логарифма данной функции ln f(x):
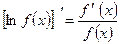
Вычисление логарифмической производной называется логарифмическим дифференцированием. Логарифмическое дифференцирование применяется при вычислении производной степенно-показательной функции, т.е. функции вида:
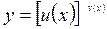
А также при нахождении производной произведения нескольких функций или производной дроби.
Пример 1. Найти производную функции 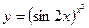
Решение.

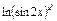 ;
; 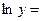
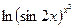
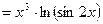
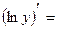
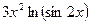
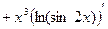 ;
; 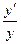
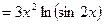
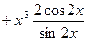
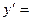
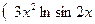
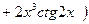
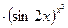
Пример 2. Найти производную функции 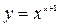
Решение:
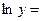
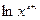 ;
; 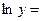
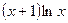
 2015-07-14
2015-07-14 1453
1453







