Дифференцируем обе части

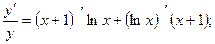
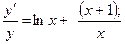
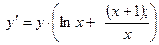
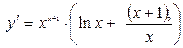
Пример 3. Найти производную функции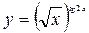

Решение:

;

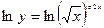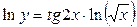
Дифференцируем обе части

;

;

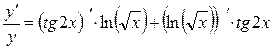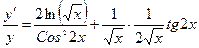
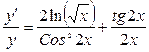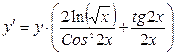
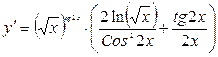
1. Производная функции, заданной параметрически.

Если функция y=y(x) задана уравнением, не разрешенным относительно y, то для нахождения производной y¢ надо продифференцировать по х обе части этого уравнения, помня, что y есть функция от х, и затем разрешить полученное уравнение относительно y¢. Чтобы найти y¢¢, надо уравнение продифференцировать дважды по х и т.д.

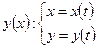
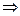
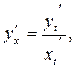
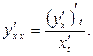
Пример 1: Дана функция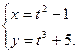

Найти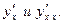

Решение.

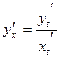
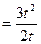
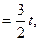
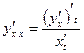
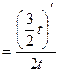
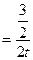
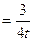
Пример 2: Найти производную 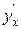, если функция задана параметрически: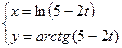

Решение:

Используем правило .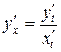

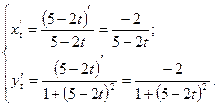
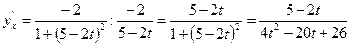
Задания

1. Продифференцировать функции, используя метод логарифмического дифференцирования.

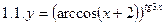
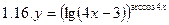
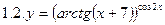
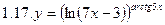
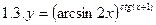
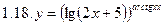
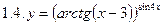
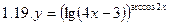
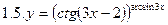
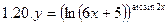
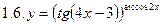
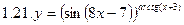
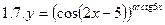
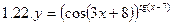
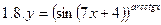
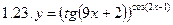
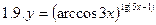
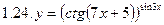
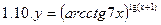
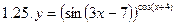
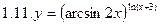
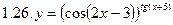
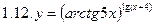
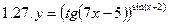
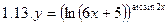
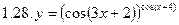
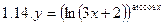
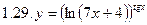
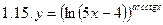
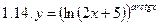
2. Продифференцировать функции, используя метод логарифмического дифференцирования.

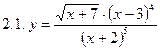
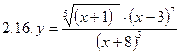
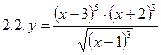
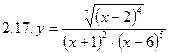
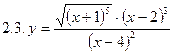
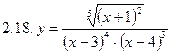
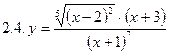
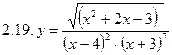
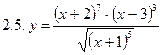
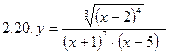
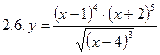
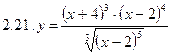
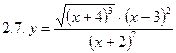
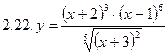
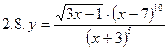
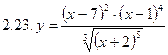
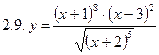
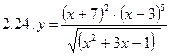
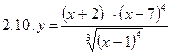
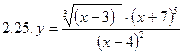
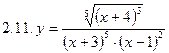
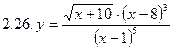
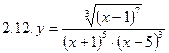
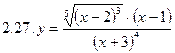
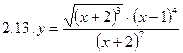
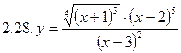
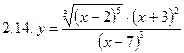
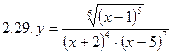
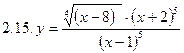
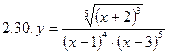
3. Найти производную неявной функции

Найти у' и у".

3.1. у² = 8xy+2x. 3.2. tg уx = 2х + 3у.

3.3. у = х + arctg у. 3.4. 6х - sin у = 4у

3.5. у² +y= 25х - 4. 3.6. arcctg y = 4x + 5y.

3.7. у² - х = cos у. 3.8. 3х + sin у = 5у.

3.9. tg у = Зх + 5у. 3.10. ху = ctg у.

3.11. у = е^y + 4х. 3.12. ln у - у/х = 7.

3.13. y² + x² = sin y. 3.14. е^y = 4х - 7у.

3.15. 4 sin²(x + y) = x. 3.16. sin y = 7x + 3y.

3.17. tg у = 4у - 5х. 3.18. у = 7х - ctg у.

3.19. ху - 6 = cos у. 3.20. 3у = 7 + ху³.

3.21. у² = х + ln (у/х). 3.22. ху² - у³ = 4х - 5.

3.23. х²у² + х = 5у. 3.24. x⁴ + х²у² + y = 4.

3.25. sin у = ху² + 5. 3.26. х³ + у³ = 5х.

3.27 cos³(2х -у²) = 7. 3.28. у² = (х-у)/(х + у).

3.29. sin²(Зх + у²) = 5. 3.30. ctg²(х + y) = 5х.