Геометрический смысл производной

Введем сначала определение касательной к кривой в данной точке.

Пусть имеем кривую и на ней фиксированную точку М₀ (см. рисунок).Рассмотрим другую точку М этой кривой и проведем секущую M₀M. Если точка М начинает перемещаться по кривой, а точка М₀ остается неподвижной, то секущая меняет свое положение. Если при неограниченном приближении точки М по кривой к точке М₀ с любой стороны секущая стремится занять положение определенной прямой М₀Т, то прямая М₀Т называется касательной к кривой в данной точке М₀.

Т.о., касательной к кривой в данной точке М₀ называется предельное положение секущей М₀М, когда точка М стремится вдоль кривой к точке М₀.

Рассмотрим теперь непрерывную функцию y=f(x) и соответствующую этой функции кривую. При некотором значении х ₀ функция принимает значение y₀=f(x₀). Этим значениям x ₀ и y ₀ на кривой соответствует точка М₀(x₀; y₀). Дадим аргументу x₀ приращение Δ х. Новому значению аргумента соответствует наращенное значение функции y ₀+Δ y=f(x ₀–Δ x). Получаем точку М(x₀ +Δ x; y₀ +Δ y). Проведем секущую М₀М и обозначим через φ угол, образованный секущей с положительным направлением оси Ox. Составим отношение и заметим, что .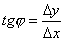

Если теперь Δ x →0, то в силу непрерывности функции Δ у →0, и поэтому точка М, перемещаясь по кривой, неограниченно приближается к точке М₀. Тогда секущая М₀М будет стремиться занять положение касательной к кривой в точке М₀, а угол φ→α при Δ x →0, где через α обозначили угол между касательной и положительным направлением оси Ox. Поскольку функция tg φ непрерывно зависит от φ при φ≠π/2 то при φ→α tg φ → tg α и, следовательно, угловой коэффициент касательной будет:

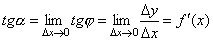
т.е. f '(x) = tg α.

Т.о., геометрически у '(x₀) представляет угловой коэффициент касательной к графику этой функции в точке x₀, т.е. при данном значении аргумента x, производная равна тангенсу угла, образованного касательной к графику функции f(x) в соответствующей точке М₀ (x; y) с положительным направлением оси Ox.

Пример. Найти угловой коэффициент касательной к кривой у = х ² в точке М (-1; 1).

Ранее мы уже видели, что (x ²)' = 2 х. Но угловой коэффициент касательной к кривой есть tg α = y '|_x=-1 = – 2.