Дифференцируемость функций. Непрерывность дифференцируемой функции

Функция y=f(x) называется дифференцируемой в некоторой точке x ₀, если она имеет в этой точке определенную производную, т.е. если предел отношения существует и конечен.

Если функция дифференцируема в каждой точке некоторого отрезка [ а; b ] или интервала (а; b), то говорят, что она дифференцируема на отрезке [ а; b ] или соответственно в интервале (а; b).

Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.

Теорема. Если функция y=f(x) дифференцируема в некоторой точке x₀, то она в этой точке непрерывна.

Доказательство. Если 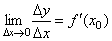, то ,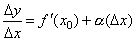

где α бесконечно малая величина, т.е. величина, стремящаяся к нулю при Δ x →0. Но тогда

Δ y = f '(x₀) Δ x +αΔ x => Δ y →0 при Δ x →0, т.е f(x) – f(x₀) →0 при x → x ₀, а это и означает, что функция f(x) непрерывна в точке x ₀. Что и требовалось доказать.

Таким образом,из дифференцируемости функции следует ее непрерывность.

Таким образом, в точках разрыва функция не может иметь производной. Обратное утверждение неверно: существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми (т.е. не имеют в этих точках производной).

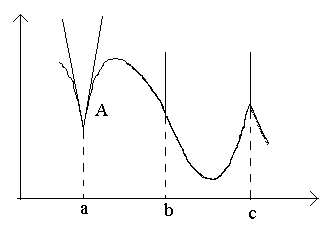Рассмотрим на рисунке точки а, b, c.

В точке a при Δ x →0 отношение не имеет предела (т.к. односторонние пределы различны при Δ x →0–0 и Δ x →0+0). В точке A графика нет определенной касательной, но есть две различные односторонние касательные с угловыми коэффициентами к ₁ и к ₂. Такой тип точек называют угловыми точками. В точке b при Δ x →0 отношение является знакопостоянной бесконечно большой величиной 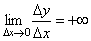. Функция имеет бесконечную производную. В этой точке график имеет вертикальную касательную. Тип точки – "точка перегиба" c вертикальной касательной.

В точке c односторонние производные являются бесконечно большими величинами разных знаков. В этой точке график имеет две слившиеся вертикальные касательные. Тип – "точка возврата" с вертикальной касательной – частный случай угловой точки.

Пример.

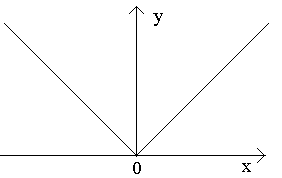
1. Рассмотрим функцию y=|x|. Эта функция непрерывна в точке x = 0, т.к. .

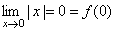Покажем, что она не имеет производной в этой точке.

f (0+Δ x) = f (Δ x) = |Δ x |. Следовательно, Δ y = f (Δ x) – f (0) = |Δ x |

Но тогда при Δ x < 0 (т.е. при Δ x стремящемся к 0 слева)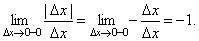

А при Δ x > 0

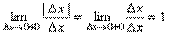
Т.о., отношение при Δ x → 0 справа и слева имеет различные пределы, а это значит, что отношение предела не имеет, т.е. производная функции y=|x | в точке x = 0 не существует. Геометрически это значит, что в точке x = 0 данная "кривая" не имеет определенной касательной (в этой точке их две).