Из физики известно, что закон равномерного движения имеет вид s = v·t, где s – путь, пройденный к моменту времени t, v – скорость равномерного движения.
Однако, т.к. большинство движений происходящих в природе, неравномерно, то в общем случае скорость, а, следовательно, и расстояние s будет зависеть от времени t, т.е. будет функцией времени.
Итак, пусть материальная точка движется по прямой в одном направлении по закону s=s(t).
Отметим некоторый момент времени t 0. К этому моменту точка прошла путь s=s(t 0 ). Определим скорость v материальной точки в момент времени t 0.
Для этого рассмотрим какой-нибудь другой момент времени t 0 + Δ t. Ему соответствует пройденный путь s =s(t 0 + Δ t). Тогда за промежуток времени Δ t точка прошла путь Δs =s(t 0 + Δ t) – s(t).
Рассмотрим отношение 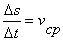 . Оно называется средней скоростью в промежутке времени Δ t. Средняя скорость не может точно охарактеризовать быстроту перемещения точки в момент t 0 (т.к. движение неравномерно). Для того, чтобы точнее выразить эту истинную скорость с помощью средней скорости, нужно взять меньший промежуток времени Δ t.
. Оно называется средней скоростью в промежутке времени Δ t. Средняя скорость не может точно охарактеризовать быстроту перемещения точки в момент t 0 (т.к. движение неравномерно). Для того, чтобы точнее выразить эту истинную скорость с помощью средней скорости, нужно взять меньший промежуток времени Δ t.
Итак, скоростью движения в данный момент времени t 0 (мгновенной скоростью) называется предел средней скорости в промежутке от t 0 до t 0+Δ t, когда Δ t →0:
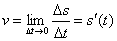 ,
,
т.е. скорость неравномерного движения это производная от пройденного пути по времени.
 2015-07-14
2015-07-14 595
595








