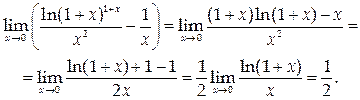
Ответ: 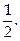
1.2.5. Формула Тейлора
Рассмотрим функцию y=f(x), имеющую в окрестности точки х=а все производные до порядка (n+ 1) включительно, и поставим задачу: найти многочлен y=Pn(x) степени не выше n, для которого его значение в точке а, а также значения его производных по n -й порядок равны значениям при x=a выбранной функции и ее производных соответствующего порядка:
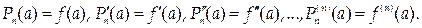
Пусть искомый многочлен имеет вид:
Pn(x)=C0+C1(x-a)+C2(x-a)²+…+Cn(x-a)n.
При этом
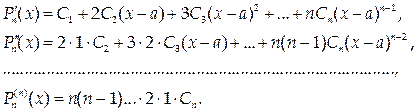
Тогда
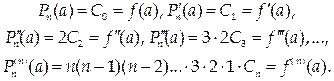
Из формул (21.3) можно выразить коэффициенты Сi через значения производных данной функции в точке а.
| Произведение последовательных натуральных чисел 1∙2∙3∙…∙(n -1) n называется факториалом числа n и обозначается n! = 1∙2∙3∙…∙(n -1) n. |
Дополнительно вводится 0!=1.
Используя это обозначение, получим:
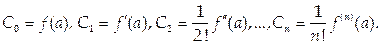
Таким образом, искомый многочлен имеет вид:
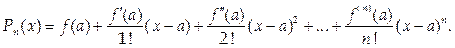
Обозначим через Rn(x) разность значений данной функции f(x) и построенного многочлена Pn(x): Rn(x) = f(x) – Pn(x), откуда f(x) = Pn(x) + Rn(x) или
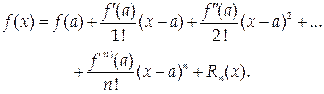
|
Полученное представление функции называется формулой Тейлора, а Rn(x) называется остаточным членом формулы Тейлора. Для тех значений х, для которых Rn(x) мало, многочлен Pn(x) дает приближенное представление функции f(x). Следовательно, формула Тейлора дает возможность заменить функцию y = f(x) многочленом y = Pn(x) с соответствующей степенью точности, равной значению остаточного члена Rn(x).
|
|
|
 2015-07-14
2015-07-14 333
333








