Найдем разложения по формуле Тейлора при а = 0 (точнее, по формуле Маклорена) функций y = ex, y = sin x, y = cos x, y = ln(1 + x), y = (1 + x) m.
1) f(x) = ех.
f(x) = f ′(x) = … = f (n)(x) = ex, следовательно, f(0) = f ′(0) = … = f(n)(0) = 1. Подставляя эти результаты в формулу Маклорена, получим
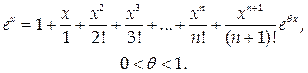
|
Отметим, что для любого х
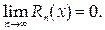
2) f(x) = sin x.
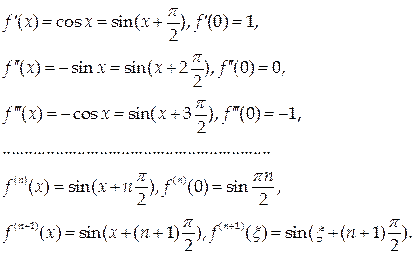
Разложение по формуле Маклорена имеет вид:
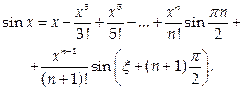
|
В этом случае, как и в предыдущем, при всех значениях х
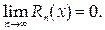
Можно предложить еще один вариант этой формулы:
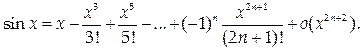
3) f(x) = cos x.
Таким же образом, как и для синуса, можно получить разложение по формуле Тейлора:
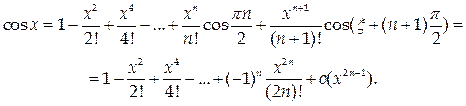
|
4) f(x) = ln(1 + x). Тогда
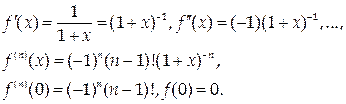
Следовательно,
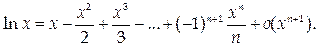
|
5) f(x) = (1 + x) m. При этом f (n)(x) = m(m - 1)…(m – n + 1)(1 + x) m-n,
f (n)(0) = m (m – 1)…(m – n +1). Тогда
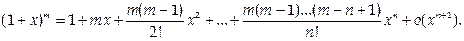
|
Применение формулы Тейлора для приближенных вычислений
Заменяя какую-либо функцию, для которой известно разложение по формуле Тейлора, многочленом Тейлора, степень которого выбирается так, чтобы величина остаточного члена не превысила выбранное значение погрешности, можно находить приближенные значения функции с заданной точностью.
Найдем приближенное значение числа е, вычислив значение многочлена Тейлора при n =8:
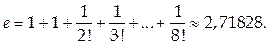
При этом
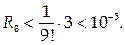
 2015-07-14
2015-07-14 332
332








