Пошук області оптимуму

Для пошуку області оптимуму можуть бути використані два методи: Гаусса-Зейделя та градієнта (рис. 10).

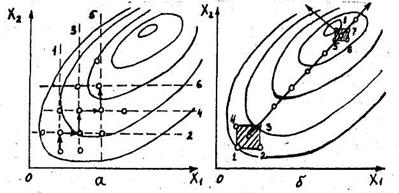
Рис. 10. Два способи пошуку оптимуму

Метод Гаусса-Зейделя полягає в тому, що спочатку послідовно змінюють значення одного фактора при фіксованих значеннях інших факторів. Після досягнення локального екстремуму фактор фіксується, починають послідовно змінювати другий фактор до досягнення локального екстремуму за цим фактором і т.д. Пояснимо цей метод за допомогою рис. 10, а. Спочатку зафіксуємо фактор х ₁ і будемо послідовно змінювати значення фактора х ₂ в напрямі 1 до досягнення локального екстремуму параметра оптимізації. Після цього зафіксуємо значення фактора х ₂ і починаємо змінювати значення фактора х ₁ у напрямі 2 до досягнення нового локального екстремуму і т.д.

Такий шлях до вершини дуже вихлястий та трудомісткий. Він є ще більш трудомістким при збільшенні кількості факторів. Тому для досягнення області оптимуму частіше використовують метод градієнта.

Відомо, що рух з деякої точки всередині області, що вивчається, у напрямі градієнта є найкоротшим шляхом до екстремуму. Графічну інтерпретацій такого руху для двох факторів показано на рис. 10, б. При використанні методу градієнта спочатку шляхом планування експерименту вивчають локальну область з дослідами 1-4. Потім знаходять напрям градієнта і в цьому напрямі ставлять подальші досліди доти, поки не буде досягнуто локального екстремуму. Якщо область оптимуму знаходиться близько, то подальші дослідження можна не проводити, а якщо оптимум далеко, то в точці локального екстремуму може бути спланована нова серія дослідів 5 - 8 і з допомогою нового напряму градієнта буде досягнуто оптимум.

Градієнт функції y є вектор

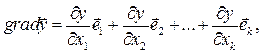
де 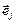- одиничні вектори у напрямах x_j.

Складові градієнта є часткові похідні функції відгуку за відповідними змінними x_j.

У лінійному рівнянні, яке використовують на першому етапі планування експерименту як модель, часткові похідні за відповідними факторами є коефіцієнтами b_j, тобто

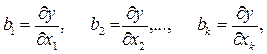
а одиничні вектори

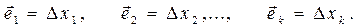
Тому для лінійного рівняння регресії

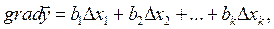
тобто для здійснення руху за градієнтом необхідно змінювати значення факторів по кожній з осей x_j пропорційно коефіцієнтам b_j.

Рух за градієнтом називають також крутим сходженням, оскільки рух відбувається по самому крутому шляху. При переході від кодованих значень D x_j до натуральних 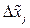напрям градієнта не змінюється, оскільки при цьому відбувається лише перехід від однієї системи координат до іншої. Такий перехід необхідний у зв’язку з тим, що експерименти повинні виконуватись при натуральних значеннях факторів.

Техніку обчислення крутого сходження зручно розглянути на прикладі одного фактора (рис. 11).

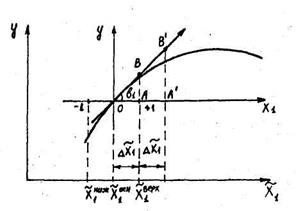
Рис. 11. Пояснення методики крутого сходження в напрямі градієнта

У цьому випадку рівняння регресії має вигляд y = b ₀+ b ₁ x ₁, тому градієнт буде задаватися рівнянням 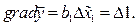Величину 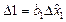, називають кроком фактора. Якщо фактор змінювати від основного рівня шляхом послідовного додавання значень кроку, то одержуватимемо координати точок, які лежать на гра­дієнті. Проводячи досліди в цих точках, будемо одержувати значення параметра оптимізації, які лежать на найкоротшому шляху до оптимуму.

Узагальнення на випадок k факторів відбувається механічно, оскільки усі фактори незалежні один від одного. Тому величину кроку для будь-якого фактора обчислюють за формулою

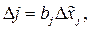
де j =1,2,…, k - номери факторів.

Якщо одержане значення кроку хоча б для одного фактора виявиться дуже великим або дуже малим, то його можна підкоригувати множенням або діленням усіх кроків на одне й те саме число. При цьому нові кроки також будуть давати точки, які лежать на градієнті. Малий крок потребує значної кількості дослідів для досягнення оптимуму, а великий крок - збільшує ймовірність проскакування області оптимуму. В усіх випадках коригування кроків потрібно виходити з того, що нижня границя задається можливістю фіксування двох сусідніх дослідів, а верхня - областю визначення фактора. Для полегшення роботи використані кроки, як правило, округлюються.

На розрахунок градієнта коефіцієнт b ₀ не впливає. Для якісних факторів, які варіюються на двох рівнях, градієнт реалізується або двічі для кожного рівня окремо, або фіксується кращий рівень і потім здійснюється круте сходження. Незначимі фактори стабілізуються на будь-якому рівні в інтервалі ±1, оскільки в русі за градієнтом вони участі не беруть. Якщо немає спеціальних міркувань, то вибирають нульовий рівень. Якщо ж за економічними міркуваннями вигідно підтримувати, наприклад, нижній рівень, то вибирають його.

Рух до області оптимуму завжди починають з нульового рівня, оскільки функція відгуку розкладалась у ряд Тейлора навколо нульової точки, тому саме до неї і відноситься оцінка градієнта.

Розглянемо приклад руху за градієнтом. Нехай потрібно знайти область оптимуму процесу розчинення CaWO₃ в HCl. Факторами цього процесу є: 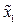- температура розчину, °С, та 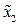- тривалість розчинення, хв. Адекватне лінійне рівняння регресії має вигляд

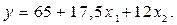
Значення рівнів факторів:

Фактори…………………………………………………………..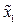
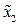
Основний рівень…………………………………………………	50 °С	30 хв
Інтервал варіювання…………………………………………….	10 °С	10 хв

Знайдемо величину кроків для кожного фактора:

3 одержаних даних випливає, що величина кроку для фактора 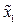дуже велика і не має фізичного змісту, оскільки при температурі 175 °С весь розчин випаровується. Тому необхідно провести корекцію кроків, поділивши їх на деяке додатне число, наприклад на 18: 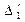=175/18=9,7 °С; 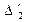=120/18=6,6 хв.

Тепер необхідно зробити другу корекцію, тобто округлити одержані значення кроків до зручних для проведення експерименту величин. А саме, 9,7 округляємо до 10°С, оскільки точність підтримання температури за умов експерименту становить ± 1°С. Значення фактора можна округлити до 5 хв, оскільки це дозволить одержати зручні умови проведення дослідів, які кратні п’яти. Умови проведен­ня дослідів на градієнті та одержані при цьому експериментальні значення параметра оптимізації наведені в табл.16.

Таблиця 16

Умови та результати руху за градієнтом

Номер досліду	Умови проведення	y,%
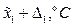
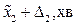
			89,0
			96,2
			98,1
			99,5
			99,9
			99,9

Після того як одержані умови проведення першого досліду, виконується цей дослід і знаходиться значення параметра оптимізації. Потім до умов проведення першого досліду алгебраїчно додають величини кроків і одержують умови проведення другого досліду. Після його проведення одержане значення параметра оптимізації порівнюють із результатом першого досліду. Якщо є збільшення (або зменшення) значення параметра оптимізації, то до умов проведення другого досліду додають величини кроків і одержують умови проведення третього досліду і т.д. доти, поки не буде одержано максимальне (або мінімальне) значення параметра оптимізації.

При русі за градієнтом може настати досягнення одним із факторів верхньої межі області його визначення. Так, наприклад, 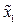не може бути більшим за 90 °С, оскільки настане зміна стану об’єкта дослідження, тобто розчин почне інтенсивно кипіти. Тому досліди 5 та 6 виконують при русі тільки за фактором 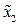доти, поки наступне значення параметра оптимізації не буде дорівнювати попередньому, або не почне зменшуватись (збільшуватись). Поява значення параметра оптимізації меншого або рівного попередньому свідчить про те, що область оптимуму досягнута і поставлене завдання щодо знаходження області оптимуму може вважатися виконаним.

При русі за градієнтом можливі п’ять ситуацій (схематично показані на рис.12).

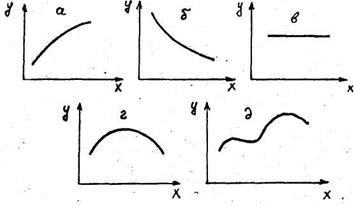
Рис.12. Ситуації при русі за градієнтом

Найбільш сприятливими є ситуації а, г, д, де рух за градієнтом є ефективним. У випадку а параметр оптимізації весь час зростає, у випадку г він проходить через максимум, що було проілюстровано прикладом. Більш складна ситуація д, де порушена передумова одноекстремальності.

Випадок б ілюструє неефективність крутого сходження. Замість очікуваного збільшення параметра оптимізації спостерігається його зменшення. Тут або план експерименту розташований в області оптимуму, або є грубі похибки.

У випадку в усі досліди на градієнті дають одне й те саме значення. Поверхня відгуку має вигляд постійного гребня.

Відповідно до крокових принципів руху по поверхні відгуку, круте сходження може здійснюватись багаторазово, поки не буде до­сягнута майже стаціонарна область (див. рис. 10, б).