Дифференциальные уравнения первого порядка в частных производных

Если в дифференциальном уравнении неизвестная функция зависит от нескольких переменных, то уравнение называется дифференциальным уравнением в частных производных. В дальнейшем считаем независимой переменной 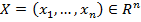, а искомой функцией – функцию .

Уравнением первого порядка в частных производных назовём уравнение вида:

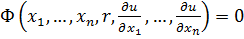, (1)

где Ф – непрерывно дифференцируемая функция своих аргументов.

Уравнение (1) называется линейным, если функция Ф линейна относительно искомой функции 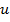и её производных:

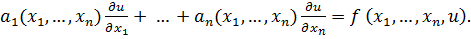(2)

Если Ф линейно зависит лишь от производных 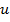, то уравнение называют квазилинейным (почти линейным):

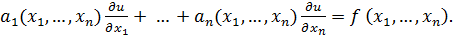(3)

В случае, когда 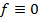линейное уравнение называют однородным, иначе – неоднородным.