Построим общее решение линейного однородного уравнения
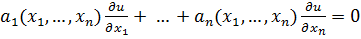 . (4)
. (4)
Уравнению (4) сопоставим систему дифференциальных уравнений
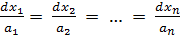 , (5)
, (5)
которую назовём характеристической. Заметим, что характеристическая система (5) содержит 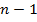 обыкновенное дифференциальное уравнение первого порядка. Значит общее решение (5) запишется в виде:
обыкновенное дифференциальное уравнение первого порядка. Значит общее решение (5) запишется в виде:
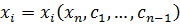 ,
, 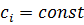 ,
, 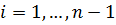 .
.
Если полученный общий интеграл разрешить относительно 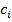 , то будем иметь
, то будем иметь 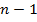 линейно независимую функцию, тождественно равную константе на любом решении системы (5):
линейно независимую функцию, тождественно равную константе на любом решении системы (5):
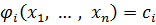 ,
, 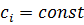 ,
, 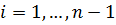 . (6)
. (6)
Каждая из функций 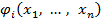 , определённая (6), называется первым интегралом уравнения (4)
, определённая (6), называется первым интегралом уравнения (4)
Первые интегралы 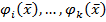 , определённые в окрестности точки называются независимыми в точке
, определённые в окрестности точки называются независимыми в точке 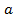 , если
, если
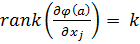 ,
, 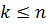 .
.
Для системы (5) существует 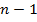 независимых первых интегралов.
независимых первых интегралов.
Общее решение линейного однородного уравнения (4) представимо в виде
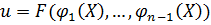 , (7)
, (7)
где 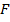 – произвольная дифференцируемая функция от
– произвольная дифференцируемая функция от 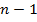 независимых первых интегралов
независимых первых интегралов 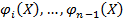 .
.
 2015-07-21
2015-07-21 415
415








