Метод простых итераций

Систему уравнений представим в виде

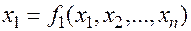
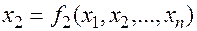
… (7.2)

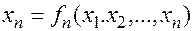
Алгоритм решения этой системы методом простых итераций напоминает метод простых итераций, используемый для решения систем линейных уравнений.

Приближение с номером k можно представить в виде

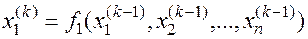
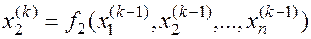
… (7.3)

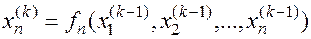
Итерационный процесс продолжается до тех пор, пока изменения всех неизвестных в двух последовательных итерациях не станут малыми, то есть до достижения заданной точности

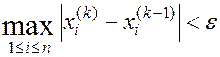
Условие сходимости выглядит для нелинейных систем следующем образом

1. Составляется матрица

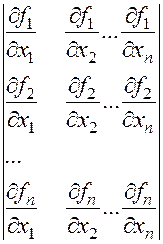
2. В выражения частных производных при вычислении значений коэффициентов матрицы используем начальное приближение

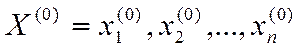
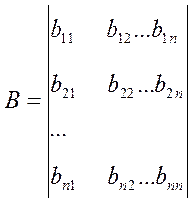
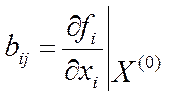
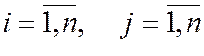
3. Определяем первую или вторую норму матрицы В соответственно

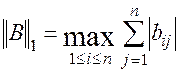
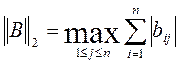
4. Условие сходимости

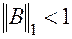
или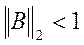

Определение начального приближения достаточно ответственный этап, так как от выбора начального приближения зависит условие сходимости итерационного процесса.

Для случая двух уравнений с двумя неизвестными начальное приближение находят графически.