Методом Эйлера

Лабораторная работа № 7. Решение систем дифференциальных уравнений

Часть 1. Приближённое решение задачи Коши

методом Эйлера

Пусть требуется найти приближённое решение дифференциального уравнения 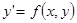, удовлетворяющее начальному условию 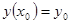. Численное решение задачи состоит в построении таблицы приближённых значений 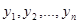решения уравнения 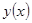в точках 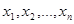. Чаще всего

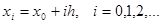(1)

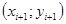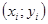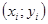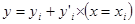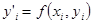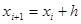Этот метод относится к группе одношаговых методов, в которых для расчёта точки требуется информация только о последней вычисленной точке . Метод допускает простую геометрическую интерпретацию (рис. 3). Предположим, что известна точка , определяется уравнением ,(в скобках не равно, а минус) а так как и , то 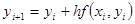. Для оценки погрешности метода на одном шаге сетки разложим точное решение в ряд Тейлора в окрестности узла :

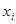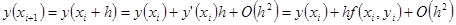. (2)

Сравнение формулы (1) с разложением (2) показывает, что они согласуются до членов первого порядка по 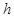, а погрешность формулы (1) равна 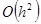. Если расчётные формулы численного метода согласуются с порядком метода. Таким образом, метод Эйлера – метод первого порядка.

Метод Эйлера легко обобщается на случай нормальных систем дифференциальных уравнений. Пусть требуется найти решение системы дифференциальных уравнений

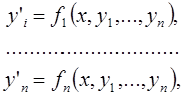
удовлетворяющее начальным условиям 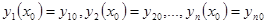. Или в векторной форме:

, ,

.

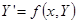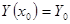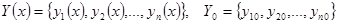Приближённые значения 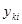точного решения 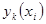в точках 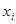вычисляются по формулам

,

,

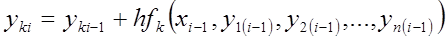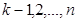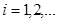
Задание. Составить программу решения задачи Коши для заданной системы дифференциальных уравнений второго порядка. Результаты печатать на каждом шаге.