| (3.12) |
Z = f (x1,x2,…, xn) max,
| (3.13) |
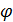 1(x1,x2,…, xn) =
1(x1,x2,…, xn) = 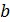 1,
1,
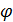 2(x1,x2,…, xn) =
2(x1,x2,…, xn) = 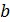 2,
2,
- - - - - - - - - - - - - - -
| (3.14) |
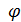 m(x1,x2,…, xn) =
m(x1,x2,…, xn) = 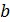 m,
m,
xj ≥ 0, j=1,2,…,n.
Вновь для решения задачи применим метод множителей Лагранжа.
Составим функцию Лагранжа
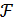 (x1,x2,…, xn, λ1, λ2,…, λm) = f (x1,x2,…, xn) +
(x1,x2,…, xn, λ1, λ2,…, λm) = f (x1,x2,…, xn) + 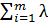 1 [b1 -
1 [b1 - 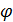 1(x1,x2,…, xn)].
1(x1,x2,…, xn)].
| (3.15) |
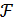 будет записываться так:
будет записываться так:
| (3.16) |
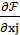 = 0, j=1,2,…,n,
= 0, j=1,2,…,n,
λi 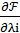 =0, i=1,2,…,m.
=0, i=1,2,…,m.
Запишем условие (3.15) в развернутом виде (случай задачи на максимум):
| (3.17) |
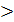 0, то
0, то 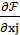 = 0; если xj
= 0; если xj 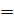 0,то
0,то 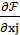 ≤ 0;
≤ 0;
или, если xj 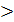 0, то
0, то 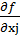 -
- 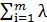 i
i 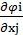 = 0; если xj
= 0; если xj 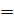 0, то
0, то 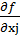 -
- 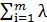 i
i 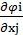 ≤ 0.
≤ 0.
Что касается условия (3.16), то относительно λi оно является тождеством. Действительно
λi 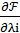 = λi (bi -
= λi (bi - 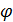 i(x1,x2,…, xn)) = 0.
i(x1,x2,…, xn)) = 0.
Согласно условию задачи 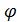 1(x1,x2,…, xn)=bi,поэтому λi (bi -
1(x1,x2,…, xn)=bi,поэтому λi (bi - 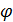 i(x1,x2,…, xn)) = 0
i(x1,x2,…, xn)) = 0
Условия bi - 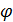 i(x1,x2,…, xn) добавляются к условиям (3.17). Получившаяся система n+m неизвестными позволит решить задачу (3.12)-(3.14).
i(x1,x2,…, xn) добавляются к условиям (3.17). Получившаяся система n+m неизвестными позволит решить задачу (3.12)-(3.14).
 2015-07-21
2015-07-21 294
294








