Задача ВП в данном случае имеет вид
| (3.28) |
| (3.29) |
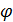 1(x1,x2,…, xn) =
1(x1,x2,…, xn) = 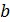 1,
1,
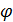 2(x1,x2,…, xn) =
2(x1,x2,…, xn) = 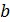 2,
2,
- - - - - - - - - - - - - - -
| (3.30) |
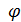 m(x1,x2,…, xn) =
m(x1,x2,…, xn) = 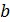 m,
m,
xj ≥ 0, j=1,2,…,n.
| (3.31) |
| (3.32) |
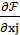 = 0, j=1,2,…,n,
= 0, j=1,2,…,n,
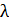 i ≥0,
i ≥0, 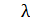 i
i 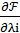 =0,
=0, 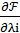 ≥0,
≥0,
где 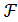 - функция Лагранжа вида
- функция Лагранжа вида
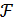 = f (x1,x2,…, xn) +
= f (x1,x2,…, xn) + 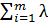 i (b i -
i (b i - 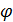 i (x1,x2,…, xn)).
i (x1,x2,…, xn)).
Если принять во внимание условие неотрицательности xj ≥ 0, j=1,2,…,n, то вместо равенств (3.31) следует пользоваться равенствами
xj 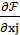 = 0, где xj ≥ 0,
= 0, где xj ≥ 0, 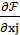 ≤ 0.
≤ 0.
С учетом вида функции Лагранжа 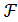 условия нахождения точка условного максимума задачи (3.28)-(3.30) можно будет записать так:
условия нахождения точка условного максимума задачи (3.28)-(3.30) можно будет записать так:
I группа условий:
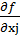 -
- 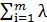 i
i 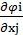 ≤ 0,
≤ 0,
(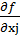 -
- 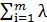 i
i 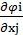 ≤ 0)xj = 0,
≤ 0)xj = 0,
xj ≥ 0, j=1,2,…,n;
II группа условий:
bi - 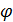 i (x1,x2,…, xn)≥0,
i (x1,x2,…, xn)≥0,
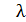 i (
i (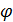 i (x1,x2,…, xn) - b1) = 0,
i (x1,x2,…, xn) - b1) = 0,
xj ≥ 0, i=1,2,…,m.
Условия I и II называются условиями Куна -Таккера. Из совокупности этих условий выделим для более глубокого рассмотрения следующие отношения.
 2015-07-21
2015-07-21 436
436








