Механическая подсистема включает элементы конструкции, которые участвуют в передаче и преобразованиях механической энергии. Свойства элементов механической подсистемы: масс, пружин, трения определяются в их компонентных уравнениях. При макромоделировании рассматривают поступательное и вращательное движение твердых тел, не имеющих пространственных размеров, т.е. материальные точки [12].
В механике поступательного движения в качестве фазовых переменных используют силу 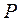 и скорость
и скорость 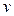 . Причем в зависимости от того, какая из них принимается за переменную типа потока, а какая за переменную типа потенциала, получаем различные модели, одинаково пригодные для анализа.
. Причем в зависимости от того, какая из них принимается за переменную типа потока, а какая за переменную типа потенциала, получаем различные модели, одинаково пригодные для анализа.
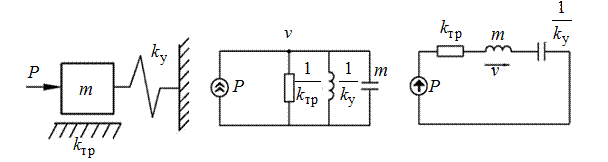
В прямой модели механической поступательной подсистемы (рис. 1.22, а) в качестве переменной типа потока выбрана сила 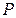 , переменной типа потенциала — скорость
, переменной типа потенциала — скорость 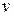 . Здесь тело массой m под действием силы P скользит по горизонтальной поверхности с коэффициентом вязкого трения k тр, преодолевая упругую силу пружины, имеющую жесткость k у.
. Здесь тело массой m под действием силы P скользит по горизонтальной поверхности с коэффициентом вязкого трения k тр, преодолевая упругую силу пружины, имеющую жесткость k у.
а) б) в)
Рис. 1.22. Кинематическая (а) и эквивалентные схемы (б,в) механического узла поступательного движения.
Законы функционирования механической подсистемы выражаются уравнениями, связывающими силы и скорости на элементах: механическом резисторе 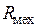 , механической индуктивности
, механической индуктивности 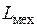 и механическом конденсаторе
и механическом конденсаторе 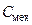 .
.
Из закона вязкого трения (сила трения прямо пропорциональна скорости движения): 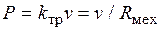 , где
, где 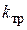 — коэффициент вязкого трения, v - относительная линейная скорость трущихся деталей, следует, что для сохранения подобия в системе по критерию
— коэффициент вязкого трения, v - относительная линейная скорость трущихся деталей, следует, что для сохранения подобия в системе по критерию 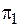 сопротивление механического резистора должно определяется соотношением
сопротивление механического резистора должно определяется соотношением 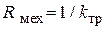 . Для механической подсистемы критерий
. Для механической подсистемы критерий 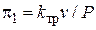 . В более общем случае сила трения имеет сложную зависимость от скорости движения (см. рис. 1.23) и содержит следующие составляющие: силу трения трогания
. В более общем случае сила трения имеет сложную зависимость от скорости движения (см. рис. 1.23) и содержит следующие составляющие: силу трения трогания 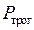 , сухое трение
, сухое трение 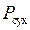 (не зависит от скорости), вязкое трение пропорциональное скорости
(не зависит от скорости), вязкое трение пропорциональное скорости 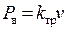 (трение Кулона) и переходную зону уменьшения силы трения после трогания (трение Штрибека).
(трение Кулона) и переходную зону уменьшения силы трения после трогания (трение Штрибека).
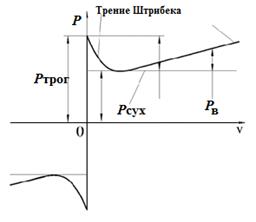
Рис. 1.23. Зависимость силы трения от скорости движения в общем случае.
Суммарную силу трения аппроксимируют следующей функцией [26]:
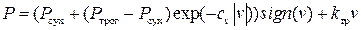 .
.
Свойства упругого элемента — пружины, отражает закон Гука: 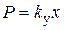 , где
, где 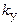 — жесткость пружины,
— жесткость пружины, 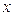 — перемещение. Или после дифференцирования по времени:
— перемещение. Или после дифференцирования по времени: 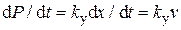 . По критерию
. По критерию 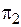 механическая индуктивность должна быть коэффициентом пропорциональности между скоростью и производной силы, т.е.
механическая индуктивность должна быть коэффициентом пропорциональности между скоростью и производной силы, т.е. 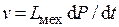 , где
, где 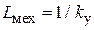 . Критерий подобия
. Критерий подобия 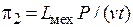 или
или 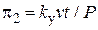 .
.
Второй закон Ньютона представляет собой уравнение для массы 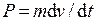 , где массу тела
, где массу тела 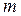 как коэффициент пропорциональности между силой и производной скорости для сохранения подобия по критерию
как коэффициент пропорциональности между силой и производной скорости для сохранения подобия по критерию 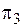 необходимо обозначить механическим конденсатором с емкостью
необходимо обозначить механическим конденсатором с емкостью 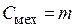 . Критерий подобия для механического конденсатора
. Критерий подобия для механического конденсатора 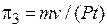 .
.
В прямой модели поступательного движения источниками фазовых переменных будут силы — аналог источника тока в электрической цепи и источник скорости — аналог источника ЭДС.
Пример эквивалентной схемы прямой модели механического узла рис. 1.22, а показан на рис. 1.22, б.
Обращенная модель механической поступательной подсистемы обосновывается для фазовых переменных типа потока — скорость 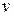 , и типа потенциала — сила
, и типа потенциала — сила 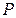 . Тогда для сохранения прежних критериев подобия получаем: для вязкого трения
. Тогда для сохранения прежних критериев подобия получаем: для вязкого трения 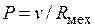 , где сопротивление механического резистора
, где сопротивление механического резистора 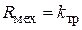 , для пружины
, для пружины 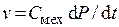 , где емкость механического конденсатора
, где емкость механического конденсатора 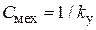 , для массы
, для массы 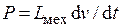 , где механическая индуктивность
, где механическая индуктивность 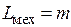 . В обращенной модели поступательного движения источниками фазовых переменных будут силы — аналог источника ЭДС в электрической цепи и источник скорости — аналог источника тока.
. В обращенной модели поступательного движения источниками фазовых переменных будут силы — аналог источника ЭДС в электрической цепи и источник скорости — аналог источника тока.
Пример эквивалентной схемы обращенной модели механического узла рис. 1.22, а показан на рис. 1.22, в.
Прямая модель вращательного движения (рис. 1.24, а) составляется с фазовыми переменными: типа потока — момент сил 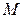 и типа потенциала — угловая скорость
и типа потенциала — угловая скорость 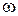 . На рисунке изображено телос моментом инерции J, которое под действием момента М вращается в подшипниках с коэффициентом вязкого трения
. На рисунке изображено телос моментом инерции J, которое под действием момента М вращается в подшипниках с коэффициентом вязкого трения 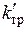 , преодолевая упругую силу пружины кручения, имеющую угловую жесткость
, преодолевая упругую силу пружины кручения, имеющую угловую жесткость 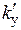 .
.
Момент вязкого трения вращательного движения определяется соотношением 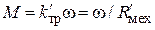 , где сопротивлениемеханического резистора
, где сопротивлениемеханического резистора 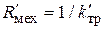 ,
, 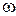 - относительная угловая скорость трущихся деталей. Критерий подобия для этого элемента
- относительная угловая скорость трущихся деталей. Критерий подобия для этого элемента 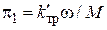 . В более общем случае зависимость силы трения вращения от угловой скорости имеет аналогичный рис. 1.23 вид при замене силы на момент, линейной скорости на угловую:
. В более общем случае зависимость силы трения вращения от угловой скорости имеет аналогичный рис. 1.23 вид при замене силы на момент, линейной скорости на угловую:
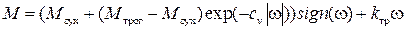 .
.
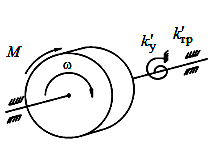 а) а) | 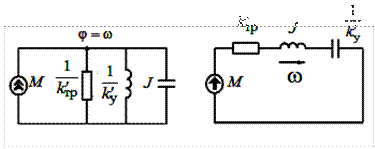 б) в) б) в) |
Рис. 1.24. Кинематическая (а) и эквивалентные схемы (б, в) механического узла вращательного движения.
Закон Ньютона вращательного движения 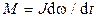 , где
, где 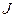 — момент инерции записывается по условиям подобия через емкость механического конденсатора:
— момент инерции записывается по условиям подобия через емкость механического конденсатора: 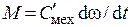 , где
, где 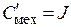 . Критерий подобия
. Критерий подобия 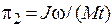 .
.
Спиральные пружины представляют упругие элементы в моделях вращательного движения. Для них справедливо уравнение 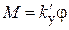 , где
, где 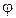 — угол закручивания. После дифференцирования, принимая во внимание, что
— угол закручивания. После дифференцирования, принимая во внимание, что 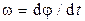 , получаем из условий подобия
, получаем из условий подобия 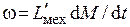 . Механическая индуктивность
. Механическая индуктивность 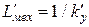 , а критерий подобия
, а критерий подобия 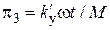 .
.
В прямой модели вращательного движения источниками фазовых переменных будут моменты — аналоги источников тока в электрической цепи и источники скорости — аналоги источников ЭДС.
Запись обращенной модели вращательного движения с фазовыми переменными типа потока — угловая скорость 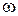 и типа потенциала — момент
и типа потенциала — момент 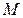 , дает следующие выражения для элементов:
, дает следующие выражения для элементов: 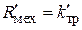 ,
, 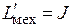 ,
, 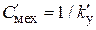 , при условии сохранения критериев подобия прямой модели. В обращенной модели вращательного движения источниками фазовых переменных будут моменты — аналоги источников ЭДС в электрической цепи и источники скорости — аналоги источников тока.
, при условии сохранения критериев подобия прямой модели. В обращенной модели вращательного движения источниками фазовых переменных будут моменты — аналоги источников ЭДС в электрической цепи и источники скорости — аналоги источников тока.
Примеры эквивалентных схем механического узла вращательного движения приведены на рис. 1.24, б, в.
В механических подсистемах электрических аппаратов имеются упоры и люфты. Упор ограничивает перемещение, и в идеальном приближении может быть представлен координатной точкой, в которой скорость движения становится равной нулю, а перемещение остается неизменным до начала движения в обратном направлении. Более точное воспроизведение процессов в механическом упоре может быть получено заменой упора нелинейной пружиной с внутренним трением. Свойства пружины – упора в виде зависимости жесткости от перемещения приведены на рис. 1.25, а. В момент касания упора в точке  наступает резкое увеличение жесткости до достижения в точке
наступает резкое увеличение жесткости до достижения в точке 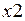 полного контакта с максимальной жесткостью
полного контакта с максимальной жесткостью
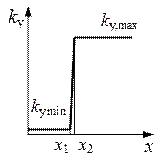 |  |
а) б)
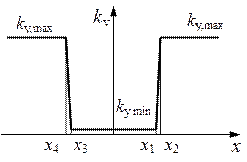
Рис. 1.25. Моделирование упора, люфта и сухого трения: а - упор; б – люфт.
Люфт в механическом соединении подвижных деталей представляют как два расположенных с малым зазором упора и моделируют нелинейной пружиной с характеристикой жесткости, представленной на рис. 1.25, б. При положительном перемещении в точке 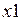 происходит касание и в точке
происходит касание и в точке 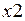 полный контакт деталей. При отрицательном перемещении аналогичные точки обозначены
полный контакт деталей. При отрицательном перемещении аналогичные точки обозначены 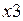 и
и 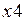 . Расстояние
. Расстояние 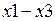 равно размеру люфта.
равно размеру люфта.
 2015-08-21
2015-08-21 1225
1225








