Погрішності квадратурних формул

Погрішності квадратурних формул, розглянутих у п.3, установлюються схожим образом. А саме, у кожному випадку визначаються локальні погрішності, які потім підсумуються.

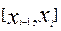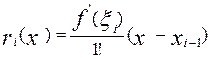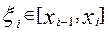
Розглянемо формулу лівих прямокутників (8). Відповідно до формули Тейлора погрішність інтерполяційної формули на відрізку становить ,де . Тоді погрішність інтегрування формули виду (4) описується вираженням

,

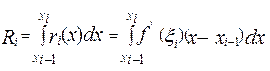яке, відповідно до узагальненої теореми про середнє значення, можна представити в більше зручній для наступного використання формі

,

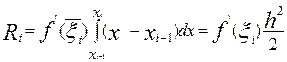де .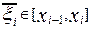

Тоді погрішність R формули (8) дорівнює

.

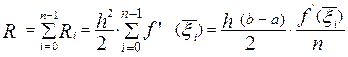Далі, припустимо функцію f(x) безперервно дифференцьована на відрізку [a, b]. Тоді по теоремі Вейерштрасса найдеться значення 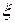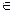[ a, b ] і вираження для опису погрішності приймає остаточний вид

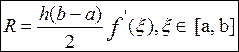. (12)

Використовуючи (12), можна вибрати крок h і число n, що забезпечують задану точність інтегрування 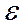. Дійсно, нехай 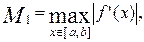, тоді

.

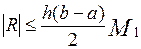Зажадавши

,

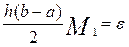одержимо

.

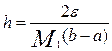Розглянемо формулу трапецій (9).

Визначимо локальну погрішність інтегрування на відрізку [ xi-1, xi]. Погрішність інтерполяції дорівнює

,

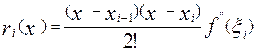де 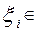[ xi-1, xi]

Тоді, відповідно до теореми про середнє значення

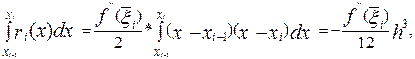
де 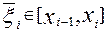. Далі, проводячи підсумовування локальних погрішностей, одержимо глобальну, що допускається на відрізку [ a, b ] при використанні формули трапеції

,

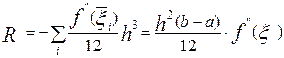де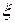

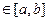
Проведемо без доказу погрішності

для правила Симпсона,-

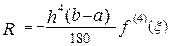
і для правила 3/8, -

.

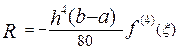Їхнє обґрунтування див. у монографії: Крилов В.И., Бобков, Монастирний. Обчислювальні методи. т2. -М.: Наука, 1977. -400с.

У висновку оборотний увагу на наступний цікавий факт. Незважаючи на більше високий ступінь інтерполяційного багаточлена, використовуваного в правилі 3/8, його підсумкова погрішність інтегрування, за інших рівних умов, вище, ніж у правилі Симпсона.