Звіт повинен містити наступні обов'язкові пункти:
- титульний лист установленого зразка;
- формулювання завдання;
- короткі теоретичні відомості про застосовувані методи;
- графіки функцій;
- результати розрахунків: ручного й за допомогою програми;
- текст програми;
- висновки.
Варіанти до завдання
1. 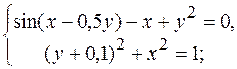
2. 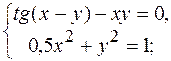
3. 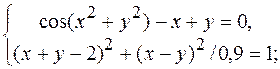
4. 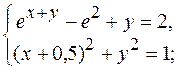
5. 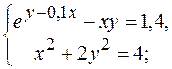
6. 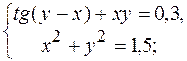
7. 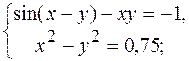
8. 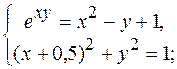
9. 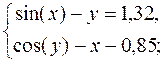
10. 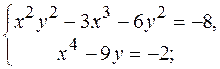
11. 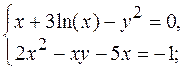
12. 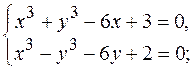
13. 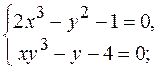
14. 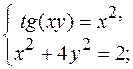
15. 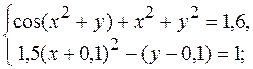
16. 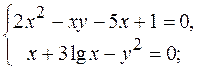
17. 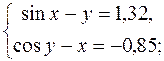
18. 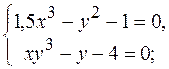
19. 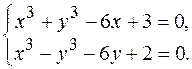
20. 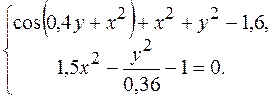
21. 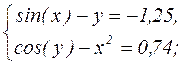
22. 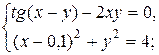
Лекція 6.. Наближене обчислення визначених інтегралів
У якій формулюються основні ідеї, реалізовані при наближеному обчисленні визначених інтегралів, розглянуті найпростіші квадратурні формули для рівновіддалених вузлів, обговорюються питання погрішності. Дано поняття про методи Монте-Карло.
6.1. Вступні зауваження
Нижче розглядаються методи наближеного інтегрування власних інтегралів Римана
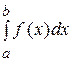 . (1)
. (1)
Традиційний підхід полягає в наступному.
На відрізку [ a, b ] вибирається ряд вузлових точок 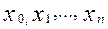 і значення інтеграла представляється у вигляді лінійної комбінації значень функції,що знаходиться під iнтегралом, у вузлових точках
і значення інтеграла представляється у вигляді лінійної комбінації значень функції,що знаходиться під iнтегралом, у вузлових точках
|
|
|
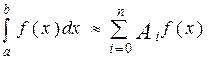 ,
,
яка називається квадратурною формулою. При заданому числі n розташування вузлів і значення коефіцієнтів 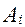 підбирається так, щоб забезпечувалася найвища точність результату. Найбільш прості й уживані методи, у яких вузлові точки вибираються рівновіддаленими. На їхньому розгляді далі ми й зупинимося.
підбирається так, щоб забезпечувалася найвища точність результату. Найбільш прості й уживані методи, у яких вузлові точки вибираються рівновіддаленими. На їхньому розгляді далі ми й зупинимося.
6.2. Формули Ньютона-Котеса
Припустимо, що відрізок [ a, b ] розділений на n рівних частин величиною 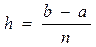 й позначимо точки ділення через
й позначимо точки ділення через 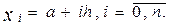 . Представимо функцію f(x) за допомогою багаточлена Лагранжа
. Представимо функцію f(x) за допомогою багаточлена Лагранжа
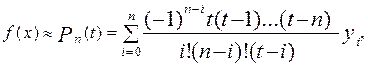
де t = 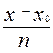 .
.
Тоді
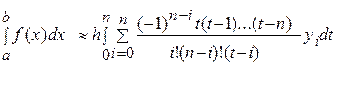 (2)
(2)
або
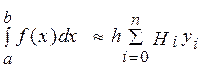 ,
,
де
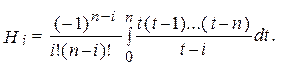 (3)
(3)
Співвідношення (2), (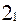 ) і називаються квадратурними формулами Ньютона-Котеса.
) і називаються квадратурними формулами Ньютона-Котеса.
У випадку, коли ділення відрізка [ a,b ] не виконується й на ньому вибирається єдина вузлова точка, позначимо її через 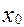 , інтерполяційний багаточлен приймає вид
, інтерполяційний багаточлен приймає вид 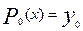 , а квадратурна формула, –
, а квадратурна формула, –
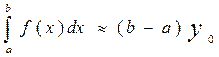 . (4)
. (4)
Розглянемо інші найпростіші випадки, попередньо обґрунтувавши важливе, для обчислення коефіцієнтів Hi, властивість:
При фіксованому n значення Hi і Hn- i, де 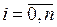 ,рівні.
,рівні.
Доказ. Нехай n=2m. Не применшуючи спільності можна вважати, що 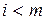 . Розглянемо чисельник функції що знаходиться під iнтегралом зі співвідношення (2)
. Розглянемо чисельник функції що знаходиться під iнтегралом зі співвідношення (2)
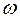 (t)=t(t-1)…(t-i)…(t-m)…(t-(2m-i))…(t-2m)...
(t)=t(t-1)…(t-i)…(t-m)…(t-(2m-i))…(t-2m)...
Видалимо з 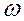 (t) множники (t-i) і (t-t-(2 m-i)) і позначимо добуток що залишилися, – через
(t) множники (t-i) і (t-t-(2 m-i)) і позначимо добуток що залишилися, – через 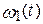 . Т.е.
. Т.е.
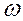 (t)=(t-i) (t-t-(2 m-i))
(t)=(t-i) (t-t-(2 m-i)) 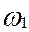 (t).
(t).
Тоді
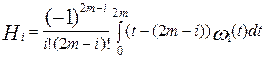
та
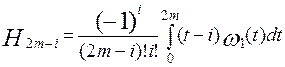
Зробимо в останніх інтегралах заміну t- m=z або t=z+m. Тоді
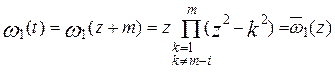
і є непарною функцією змінної z. Вираження для визначення 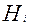 ,
, 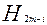 після очевидних перетворень приймуть вид
після очевидних перетворень приймуть вид
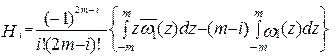 ,
,
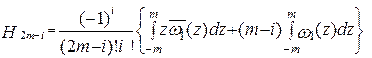 .
.
Другі доданки у фігурних дужках, у силу непарності 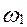 (z), рівні 0, а числа 2 m-i і i мають однакову парність. Тому
(z), рівні 0, а числа 2 m-i і i мають однакову парність. Тому 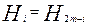 , що й було потрібно.
, що й було потрібно.
|
|
|
Випадок n=2m + 1 розглядається аналогічно.
Повернемося до обчислення коефіцієнтів 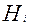 .
.
Розглянемо n=1. Тоді з (3) треба
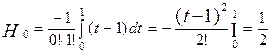 .
.
Звідси 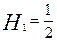 й квадратурна формула (2) приймає вид
й квадратурна формула (2) приймає вид
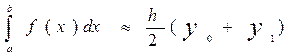 (5)
(5)
Нехай тепер n=2 З (3) маємо
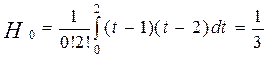 ,
,
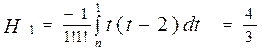 .
.
Тоді
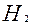 =
= 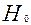 =
= 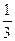
и
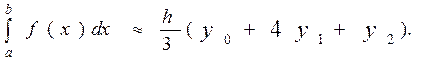 (6)
(6)
Розглянемо n=3. Згідно (3)
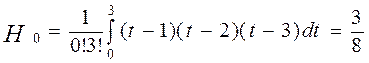 ,
,
отже, і 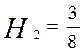 ,
,
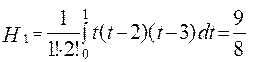 ,
,
отже, і 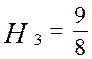 .
.
Тоді квадратурна формула (2) приймає вид
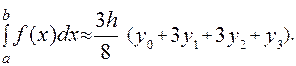 (7)
(7)
 2015-08-21
2015-08-21 277
277








