Поняття про методи Монте-Карло

Методи Монте-Карло наближеного обчислення інтегралів засновані на використанні рівномірно розподілених послідовностей.

Розглянемо на площині деяку обмежену область D площею 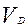й припустимо, що в ній задана деяка нескінченна послідовність точок 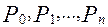,…...Нехай 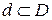деяка довільна область площею 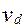. Розглянемо перші N крапок послідовності {Pi} і позначимо через 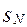число точок з них, що попадають в d. Тоді

Послідовність {Pi} рівномірно розподілена в D тоді й тільки тоді, коли

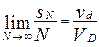
для довільної області 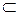d D.

Звідси треба, що при досить більших значеннях N відношення

,

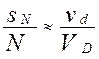звідки площа області приблизно дорівнює

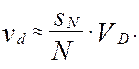(13)

Таким чином, якщо площа області D відома, то, генеруючи в ній рівномірно розподілену послідовність, площу довільної області, розташованої в ній, можна визначити простим підрахунком числа точок приналежних послідовністi {Pi}.

На цих особливостях і базуються методи наближеного інтегрування Монте-Карло.

Розглянемо інтеграл (1) і для спрощення припустимо, що f(x) 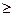0. Тоді, значення (1) являє собою площа криволінійної фігури, обмеженої графіком y=f(x), x 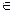[ a, b ]. Візьмемо як область D прямокутник [ a, b; 0, M ], де M 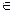max f(x,) площею 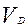= M(b-a) . Далі формуючи в D рівномірно розподілену послідовність і здійснюючи підрахунок 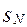,– числа точок приналежних фігурi, обмежену графіком y=f(x), по формулі (13) визначимо наближене значення площі й, тим самим, наближене значення інтеграла(1).

Відомі різні способи генерування рівномірно розподілених послідовностей, зокрема, випадково розподілені, 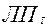– послідовності. Більш докладно про їх див. Соболь I.М., Статников Р.Б. Вибір оптимальних параметрів у задачах з багатьма критеріями.-М.: Наука, 1981. -110стор.