Пример применения модели Харрода-Домара

Рассмотрим варианты траекторий основных макроэко­номических показателей в модели Харрода — Домара при различных условиях темпа потребления.

Пусть динамика потребления C(t)=C(0)∙e^rt, а динамика ВВП

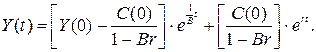
Начальные условия Y(0) = 2000 и С(0) = 400. Тогда норма потребления

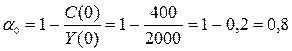
Коэффициент приростной капиталоемкости B = 2.

Вариант а) — темп прироста потребления r = 0,85.

Траектория ВВП при заданных условиях

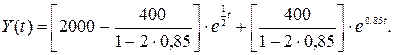
Найдем момент времени, когда Y(t)=0. Решая данное уравнение, получим

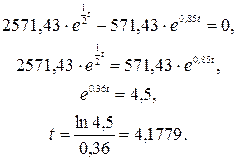
Найдем момент времени, когда выпуск продукции будет максимальным, т. е. Y’(t) = 0. Решая данное уравнение находим:

,

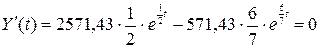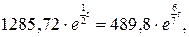
таким образом найдем момент времени при котором уровень ВВП будет максимальным,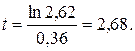

Уравнение, отражающее динамику инвестиций:

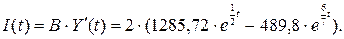
Момент времени, при котором инвестиции будут равны 0, т.е. I(t)=0 равен t =2,68.

Используя возможности приложения Microsoft Office Excel построим траекторию основных показателей.

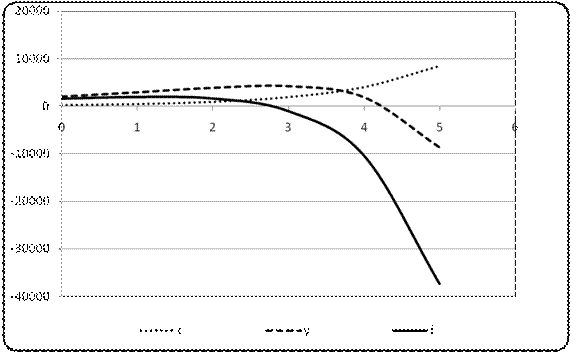
Рисунок 4.1 – Траектории функции выпуска продукции, инвестиций и потребления при значении темпа прироста r=0,85

Вариант б) — темп прироста потребления r = 0,45.

Таким образом, выполняется условие 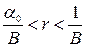. Траектория ВВП при заданных условиях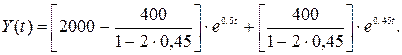

Найдем момент времени, когда Y(t) = 0, т. е.

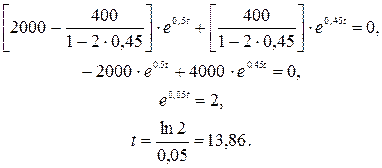
Найдем момент времени, когда выпуск продукции будет максимальным, т. е. Y’(t) = 0. Тогда

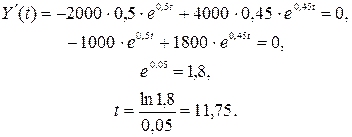
Траектории основных показателей приведенынарисунке 4.2. Как видно из рисунка и результатов расчета, период «существования» данной эконо­мической системы при новых условиях увеличился, однако темп при­роста потребления все еще высокий по сравнению с оптимальным.

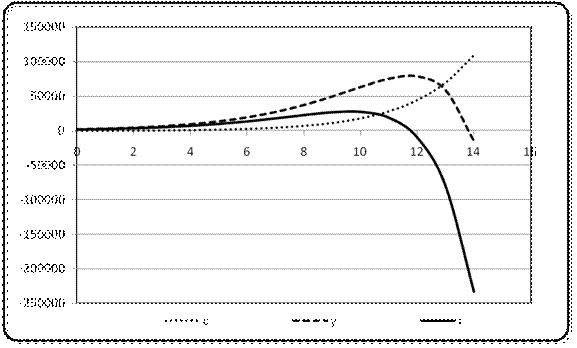
Рисунок 4.2. Траектории функций выпуска продукции, инвестиций и потребления при значении темпа прироста потребления r – 0,45

Вариант в) темп прироста потребления r = 0,4.

Таким образом, темп прироста потребления совпадает с оптимальным, т. е. 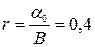(α₀ = 0,8; B= 2). Траектория выпуска продукции будет отображена моделью 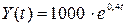. Динамика инвестиций — соответственно 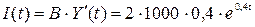; а уравнение потребления будет выглядеть так: 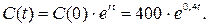Траектории основных показателей приведены на рисунке4.3.

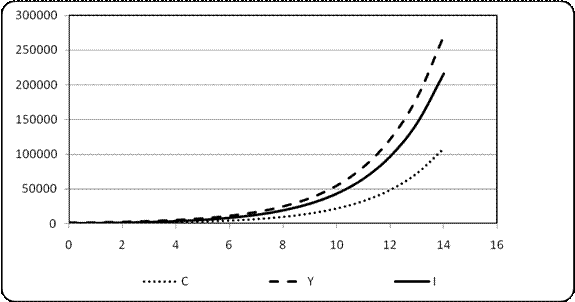
Рисунок 4.3. Траектории функций выпуска продукции, инвестиций и потребления при значении темпа прироста потребления r = 0,4

Поскольку функции выпуска, инвестиций и потребления не равны во времени, то представляет интерес сравнение накопления (суммарных) за определенный период времени показателей Y^н,I, С^н (значения определенных интегралов для представленных вариантов модели а — в).