1.Первообразная. Неопределенный интеграл его свойства.
Определение. Пусть функция 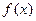 определена на некотором (конечном или бесконечном) интервале
определена на некотором (конечном или бесконечном) интервале 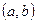 . Тогда функция
. Тогда функция 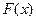 называется первообразной для функции
называется первообразной для функции 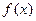 на интервале
на интервале 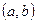 , если
, если 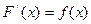 для всех
для всех 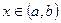 .
.
Зная только одну первообразную 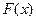 для функции
для функции 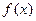 , находим множество всех первообразных для этой функции, которое совпадает с множеством функции вида
, находим множество всех первообразных для этой функции, которое совпадает с множеством функции вида 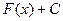 , где С -произвольная постоянная.
, где С -произвольная постоянная.
Обозначения: 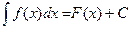 .
.
Основные свойства неопределенного интеграла:
10. 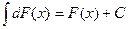 ; 20.
; 20. 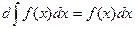
30. 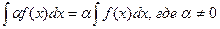
40. 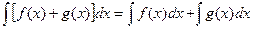
50. Если 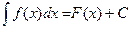 , то
, то 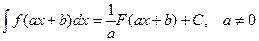 .
.
2. Основные формулы интегрирования.
Следующие интегралы обычно называются табличными интегралами:
1. 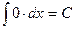 7.
7. 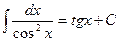
2. 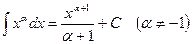 8.
8. 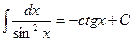
3. 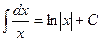 9.
9. 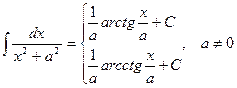
4. 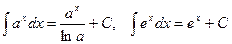 10.
10. 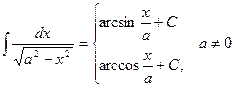
5. 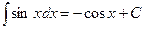 11.
11. 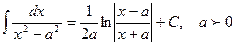
6. 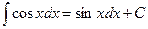 12.
12. 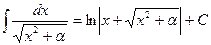
2. Интегрирование посредством разложения подынтегральной функции на слагаемые.
Рассмотрим этот метод на примере:
Пример 1. 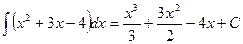
3. Интегрирование посредством замены переменной.
Пусть требуется вычислить интеграл 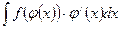 , при этом функции
, при этом функции 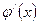 и
и 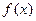 непрерывны на заданном интервале. Тогда этот интеграл можно упростить с помощью подстановки
непрерывны на заданном интервале. Тогда этот интеграл можно упростить с помощью подстановки 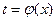 , используя равенство
, используя равенство
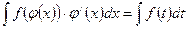 . Эта формула называется формулой замены переменной в неопределенном интеграле.
. Эта формула называется формулой замены переменной в неопределенном интеграле.
4. Интегрирование по частям.
Пусть производные функций 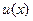 и
и 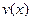 существуют и непрерывны на заданном интервале. Тогда имеет место равенство:
существуют и непрерывны на заданном интервале. Тогда имеет место равенство:

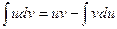 .
.
Эта формула называется формулой интегрирования по частям.
 2015-08-21
2015-08-21 215
215







