Краткое содержание лекции
Определение.Криволинейной трапецией называется область на плоскости 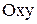 , ограниченная осью
, ограниченная осью 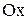 , прямыми
, прямыми 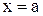 ,
, 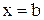 , где
, где 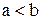 и графиком непрерывной на
и графиком непрерывной на 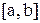 функции
функции 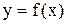 (см. рис 1).
(см. рис 1).
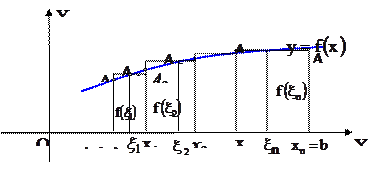
Рис 1
Теорема 1. Если функция 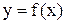 непрерывна на
непрерывна на 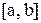 или имеет на этом отрезке конечное число точек разрыва первого рода, то эта функция интегрируема на
или имеет на этом отрезке конечное число точек разрыва первого рода, то эта функция интегрируема на 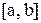 , т.е.
, т.е. 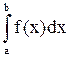 существует.
существует.
Свойства определенного интеграла
В дальнейшем будем считать, что все рассматриваемые функции интегрируемы.
1) 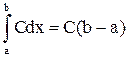 ,
, 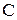 - постоянная.
- постоянная.
2) Если 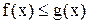 на
на 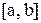 , то
, то 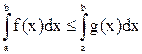 .
.
3) Если на отрезке 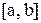 функция
функция 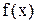 ограничена снизу и сверху числами
ограничена снизу и сверху числами 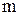 и
и 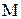 , т.е. если на
, т.е. если на 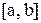
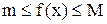 , то
, то 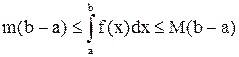 .
.
Пример 1. Оценим интеграл 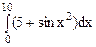 .
.
Поскольку 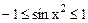 , то
, то 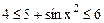 . Следовательно,
. Следовательно, 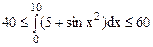 .
.
4) Теорема о среднем. Пусть функция 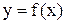 непрерывна на отрезке
непрерывна на отрезке 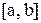 , тогда на этом отрезке найдется такая точка
, тогда на этом отрезке найдется такая точка 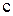 , что
, что 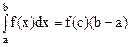 .
.
5) 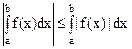 . Это свойство называется оценкой модуля определенного интеграла.
. Это свойство называется оценкой модуля определенного интеграла.
6) Если выполняется неравенство 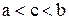 , то
, то 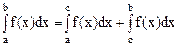 .
.
 2015-08-21
2015-08-21 292
292








