2015-08-21
225
Теорема. Пусть функция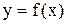 
непрерывна на отрезке 
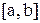, а функция 
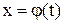монотонна и непрерывно дифференцируема на отрезке 
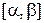, где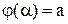 
, 
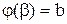, тогда
.
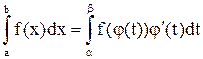Пример2. Вычислить интеграл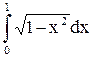 
с помощью замены переменной 
:
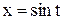Задание на СРС
1. Основные свойства определенного интеграла. Метод и интегрирования по частям в определенном интеграле. (конспект) [1,4,5].
2. Решение задач по теме [2. ИДЗ-9.1 №1, 3, 5].
