Вывод уравнений пограничного слоя

Вопрос №1

Пограничный слой. Уравнения пограничного слоя. Отрыв пограничного слоя от стенки.

Вывод уравнений пограничного слоя

Рассмотрим течение жидкости при очень малой вязкости или, в более общем виде, для случая очень большого числа Рейнольдса.

Остановимся на простом примере плоского течения около тон­кого цилиндрического тела (рис. 1.1). На некотором расстоянии от поверх­ности тела внутри жидкости преобладают, вследствие малой вязкости, силы инерции, действие же вязкости там почти не проявляется. Скорость течения почти до самой поверхности тела имеет порядок скорости V вдали от тела. Картина линий тока, а также распределение скоростей внутри жидкости практически имеют такой же вид, как и при потенциальном течении жидкости без трения. Однако более точные наблюдения пока­зывают, что жидкость не скользит по поверхности тела, как при потен­циальном течении, а прилипает к ней. Переход от нулевой скорости на стенке к полной скорости, существующей на некотором расстоянии от стенки, совершается в очень тонком слое, называемом пограничным слоем или слоем трения. Следовательно, мы должны различать в рассмат­риваемом течении две области, между которыми, правда, нельзя провести резкой границы:

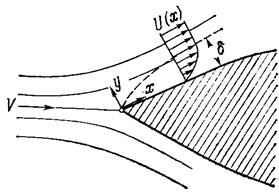
Рис. 1.1. Пограничный слой на стенке.

1. Первая область — очень тонкий слой в непосредственной близости от тела. В этой области градиент скорости ¶ и /¶ у в направлении, пер­пендикулярном к стенке, очень велик (пограничный слой), а вязкость m, как бы она ни была мала, оказывает существенное влияние на течение, поскольку здесь касательное напряжение t = m ¶ и/ ¶ у, вызванное тре­нием, может принимать большие значения.

2. Вторая область — все остальное течение вне пограничного слоя. В этой области градиент скорости не достигает таких больших значений,

как в пограничном слое, поэтому действие вязкости здесь не играет роли и можно считать, что течение здесь потенциальное.

Как правило, пограничный слой тем тоньше, чем меньше вязкость

или, в более общей формулировке, чем больше число Рейнольдса. На основании некоторых точных решений уравнений Навье — Стокса известно, что толщина пограничного слоя пропорциональна корню квадратному из кинематической вязкости, т.е.

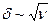
Далее, при упрощениях, которые несколько ниже будут сделаны в урав­нениях Навье — Стокса с целью получения из них уравнений погранич­ного слоя, принимается, что толщина пограничного слоя очень мала по сравнению с некоторым характерным ли­нейным размером L тела, т.е.

d << L

Приступим теперь к упрощению уравне­ний Навье — Стокса для течения в погранич­ном слое. Для этой цели прежде всего произведем оценку отдельных членов этих уравнений с точки зрения порядка их величины. Напомним, что мы рассматриваем сейчас двумерную задачу. Примем сначала, что обтекаемая жидкостью стенка плоская (см. рис. 1.1). Направим ось х вдоль стенки, а ось у - перпендикулярно к стенке. Перепишем уравнения Навье — Стокса в безразмерной форме, для чего все скорости отнесем к скорости V набегающего потока, а все длины - к характерному линейному размеру тела L, который выберем так, чтобы безразмерная величина ¶ и /¶ х в рассматриваемой области течения не превышала по порядку единицу. Давление и время сделаем безразмер­ными, разделив их соответственно на rV ² и на L / V. Полученные безраз­мерные величины обозначим для упрощения записи опять теми же бук­вами. Наконец, введем число Рейнольдса

,

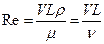которое, согласно нашему основному предположению, должно быть очень велико. В результате уравнения Навье — Стокса для рассматриваемой плоской задачи примут вид:

для направления х 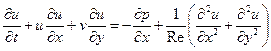, (1.1)

1 1 1 d 1/d d² 1 1/d²

для направления у 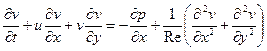, (1.2)

d 1 d d 1 d² d 1/d

Безразмерным уравнением неразрывности будет

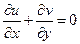(1.3)

1 1

Граничными условиями будут: прилипание жидкости к стенкам, т.е.

u = v = 0 при у = 0,

и совпадение скорости u на внешнем крае пограничного слоя со ско­ростью U внешнего течения, т.е.

u = U при у ® ¥.

Разделим толщину пограничного слоя d на характерный линейный размер тела L, т.е. сделаем эту толщину безразмерной. Такая безразмер­ная толщина - будем обозначать ее той же буквой d - на основании сделанного выше предположения должна быть весьма мала по сравнению с единицей, т.е.

d << 1

Приступим теперь к оценке отдельных членов уравнений (1.1), (1.2) и (1.3) с целью отбросить численно малые члены и тем самым упростить уравнения. Из уравнения неразрывности сразу видно, что, поскольку величина ¶ u /¶ х имеет порядок единицы, такой же порядок имеет и вели­чина ¶ v /¶ y. Но так как на стенке скорость v = 0, то отсюда следует, что в пограничном слое величина скорости v имеет порядок d. Поэтому такой же порядок d имеют в пограничном слое и величины ¶ v /¶ x и ¶² v /¶ x ². Величина ¶² u /¶ x ² имеет порядок единицы. Полученные в результате этой оценки порядки подписаны в уравнениях (1.1) - (1.3) под соответствую­щими величинами.

Далее, примем, что величина локального ускорения ¶ u /¶ t имеет такой же порядок, как и величина конвективного ускорения u ¶ u /¶ х. Это означает, что очень внезапные ускорения, например подобные тем, которые возникают при сильных волнах давления, исключаются из рас­смотрения. Члены, зависящие от вязкости, входят в уравнения (1.1) и (1.2) с малым множителем 1/Re. Тем не менее некоторые из этих членов должны быть, на основании предыдущих рассуждений, по своей величине одного порядка с инерционными членами по крайней мере в непосредственной близости от стенки. Следовательно, в близком к стенке слое жидкости некоторые из вторых производных скорости должны быть очень велики. Согласно сказанному выше такими производными могут быть только ¶² u /¶ y ² и ¶² v /¶ y ². Так как составляющая скорости, параллельная стенке, изменяется в тонком слое, имеющем толщину d, от нуля на стенке до еди­ницы на границе с внешним течением, то

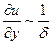и ,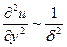

в то время как

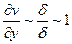и

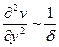
Подписав эти оценки под соответствующими величинами в уравнениях (1.1) и (1.2), мы увидим из первого уравнения, что величина членов, зависящих от вязкости, имеет в пограничном слое одинаковый порядок с инерционными членами только при условии, что величина числа Рейнольдса

имеет порядок 1/d², т.е. при условии, что

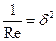(1.4)

Таким образом, для течения, в котором число Рейнольдса велико, можно упростить первое уравнение движения, отбросив для этого вели­чину ¶² u /¶ х ², как малую по сравнению с ¶² u /¶ y ². Уравнение неразрывности остается для больших Re неизменным. Что касается второго уравнения движения, то из него видно, что величина ¶ р /¶ у имеет порядок d; следова­тельно, величина разности давлений поперек пограничного слоя, которую можно было бы вычислить путем интегрирования второго уравнения, имеет порядок d², т.е. очень мала, и поэтому давление в поперечном направлении пограничного слоя остается практически постоянным. Его можно принять равным тому давлению, которое существует на внешнем крае пограничного слоя и которое определяется здесь течением без тре­ния. Таким образом, давление в пограничном слое как бы создается внеш­ним течением, и его следует рассматривать как известную функцию, зави­сящую только от продольной координаты х и от времени t.

На внешней границе пограничного слоя продольная скорость и пере­ходит в скорость U (x, t) внешнего течения. Так как здесь уже нет силь­ного градиента скорости в направлении, перпендикулярном к стенке, то теперь в уравнении (1.1) при большом числе Рейнольдса отпадают все члены, зависящие от вязкости. Поэтому для внешнего течения уравне­ние (1.1), если вернуться опять к размерным величинам, принимает вид

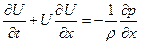(1.5)

Для стационарного течения ¶ U /¶ t = 0, а давление зависит только от х, и уравнение (1.5) принимает после замены частных производных на обыкновенные еще более простой вид:

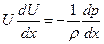(1.5а)

Проинтегрировав это уравнение, мы получим уравнение Бернулли

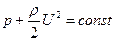(1.6)

Граничные условия для внешнего течения приближенно такие же, как для течения без трения. Пограничный слой очень тонок, а поперечная ско­рость v на его внешнем крае очень мала (v / V ~ d/ L). Следовательно, потенциальное обтекание рассматриваемого тела, имеющее на стенках тела нормальную составляющую скорости, равную нулю, можно рас­сматривать как весьма хорошее приближение для внешнего течения вяз­кой жидкости. Поэтому для определения перепада давления в продольном направлении пограничного слоя достаточно составить уравнение Бернул­ли (1.5) для совпадающей со стенкой линии тока потенциального течения, считаемого заданным.

Итак, после всех выполненных упрощений от двух уравнений Навье — Стокса остается только одно, которое, если опять вернуться к размерным величинам, принимает вместе с уравнением неразрывности следующий вид:

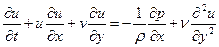, (1.7)

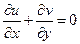, (1.8)

причем граничными условиями будут

u = v = 0 при y = 0; u = U (x, t) при у = ¥. (1.9)

Система уравнений (1.7) и (1.8) называется уравнениями Прандтля для пограничного слоя. Скорость U (x, t) потенциального течения следует рассматривать как известную функцию, определяющую посредством уравнения (1.5) распределение давления. Кроме того, для момента вре­мени t = 0 должно быть задано соответствующее условиям задачи течение в пограничном слое во всей области рассматриваемых значений х и у.

Для стационарного течения система уравнений (1.7) и (1.8) прини­мает более простой вид:

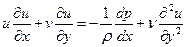, (1.10)

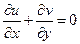, (1.11)

причем граничными условиями будут

u = 0, v = 0 при y = 0; u = U (x) при у = ¥. (1.12)

Кроме того, в начальном поперечном сечении х = х ₀ должен быть задан начальный профиль скоростей u (х ₀, у). Следовательно, задача расчета течения в пограничном слое сводится к расчету дальнейшего развития заданного начального профиля продольных скоростей при заданном потенциальном течении.

Упрощение уравнений Навье — Стокса, полученное Прандтлем, с математической точки зрения весьма значительно. Правда, теперь, в противоположность дифференциальным уравнениям ползущего движе­ния, сохраняется нелинейный характер уравнений Навье — Стокса, однако из трех первоначальных уравнений плоской задачи с переменными u,v,p одно уравнение, а именно уравнение движения для направления, перпендикулярного к стенке, полностью отпадает. Соответственно этому сокращается на единицу число неизвестных, и остается система уравнений только с двумя неизвестными u и v. Давление р уже не является неизвест­ной величиной, так как оно может быть определено из уравнения Бернулли, составленного для потенциального течения около рассматриваемого тела, причем это течение следует считать заданным. Кроме того, в един­ственном из оставшихся уравнений движения один из двух членов, зави­сящих от вязкости, теперь отсутствует.

В заключение заметим, что из формулы (1.4) получается следующая оценка для толщины пограничного слоя:

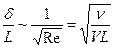, (1.13)

что подтверждает прежнюю оценку 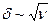, полученную из точных ре­шений уравнений Навье — Стокса. Ниже мы увидим, что для случая пластины, обтекаемой параллельно своей плоскости, численный мно­житель, переводящий пропорциональность (1.13) в равенство, равен при­ближенно 5 при условии, что L обозначает расстояние от передней кром­ки пластины.

Предыдущие рассуждения были проведены для плоской стенки. Однако они легко переносятся на случай искривленных стенок. При этом выясняется, что уравнения пограничного слоя (1.10) - (1.12) сохра­няют свою применимость, правда, при условии, что радиус кривизны стенки не претерпевает очень больших изменений, как это имеет место, например, на острых кромках.