Примеры числовых множеств
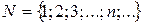 - множество натуральных чисел.
- множество натуральных чисел.
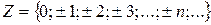 - множество целых чисел.
- множество целых чисел.
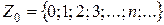 - множество целых неотрицательных чисел.
- множество целых неотрицательных чисел.
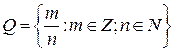 - множество рациональных чисел.
- множество рациональных чисел.
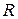 - множество действительных чисел.
- множество действительных чисел.
Свойства множества действительных чисел
Множество 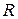 действительных чисел обладает следующими свойствами.
действительных чисел обладает следующими свойствами.
1. Оно упорядоченное: для двух любых различных чисел 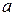 и
и 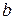 имеет место одно из двух соотношений
имеет место одно из двух соотношений 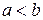 либо
либо 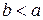 .
.
2. Множество 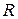 плотное: между любыми двумя различными числами
плотное: между любыми двумя различными числами 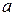 и
и 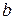 (
(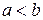 ) содержится бесконечное множество действительных чисел
) содержится бесконечное множество действительных чисел 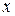 , удовлетворяющих неравенству
, удовлетворяющих неравенству
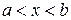 .
.
3. Множество 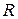 непрерывное.
непрерывное.
Пусть множество 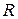 разбито на два непустых подмножества
разбито на два непустых подмножества 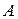 и
и 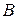 таких, что каждое действительное число содержится только в одном классе и для каждой пары чисел
таких, что каждое действительное число содержится только в одном классе и для каждой пары чисел 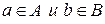 выполняется неравенство
выполняется неравенство 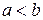 .
.
Тогда (свойство непрерывности) существует единственное число 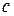 , удовлетворяющее неравенству
, удовлетворяющее неравенству
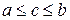 (
(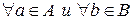 ).
).
Оно отделяет числа из классов 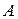 и
и 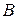 . Число
. Число 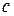 является либо наибольшим числом в классе
является либо наибольшим числом в классе 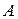 (тогда в классе
(тогда в классе 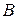
 нет наименьшего числа) либо наименьшим числом в классе
нет наименьшего числа) либо наименьшим числом в классе 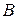 (тогда в классе
(тогда в классе 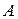
 нет наибольшего числа).
нет наибольшего числа).
1.2. Функции заданные явно и неявно и параметрически
Функция называется явнозаданной, если действия, выполняемые для ее вычисления, указаны и можно их осуществить для 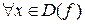 .
.
Функция может быть задана неявно. Форма ее задания в имеет вид
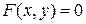 , (1)
, (1)
где 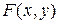 - символ функции двух аргументов, заданной явно.
- символ функции двух аргументов, заданной явно.
Например,
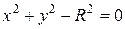 .
.
Теперь нет явного правила вычисления функции 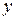 по ее аргументу
по ее аргументу 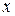 . Однако, в этом случае оно может быть легко получено в виде
. Однако, в этом случае оно может быть легко получено в виде
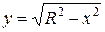 или
или 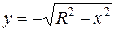 .
.
Под неявно заданной функцией
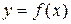
понимается такая, подстановка которой в уравнение (1) обращает его в тождество
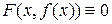 .
.
Зависимость 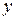 от
от 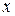 можно задать с помощью третьей переменной
можно задать с помощью третьей переменной 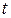 в виде
в виде
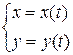 ,
,
где 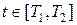 .
.
Этот способ задания функции называется параметрическим. В частности при 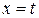 получается
получается 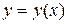 - явный способ задания функции.
- явный способ задания функции.
2. Графики элементарных функций
2.1. Степенная функция
Степенная функция задается следующим аналитическим выражением:
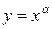 , (1)
, (1)
где 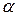 - действительное число[2].
- действительное число[2].
Область определения 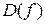 степенной функции зависит от значения показателя степени
степенной функции зависит от значения показателя степени 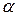 . Например, если
. Например, если 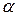 - целое положительное (натуральное) число, то областью определения степенной функции является множество действительных чисел
- целое положительное (натуральное) число, то областью определения степенной функции является множество действительных чисел 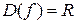 . В этом случае получается следующий ряд степенных функций:
. В этом случае получается следующий ряд степенных функций: 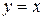 ,
, 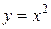 ,
, 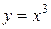 … Степенные функции с нечетными показателями степени являются нечетными, а с четными показателями степени – четными. Графики некоторых нечетных функций приведены на рис. 1, а четных – на рис. 2.
… Степенные функции с нечетными показателями степени являются нечетными, а с четными показателями степени – четными. Графики некоторых нечетных функций приведены на рис. 1, а четных – на рис. 2.
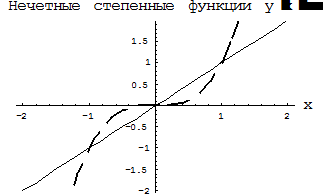
Рис. 1. 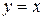 - сплошная линия,
- сплошная линия, 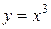 - пунктирная линия
- пунктирная линия
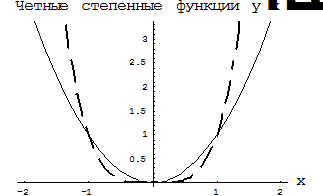
Рис. 2. 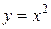 - сплошная линия,
- сплошная линия, 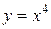 - пунктирная линия
- пунктирная линия
Если 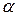 - целое отрицательное число, то в этом случае степенная функция определена для всех действительных значений
- целое отрицательное число, то в этом случае степенная функция определена для всех действительных значений 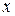 , кроме
, кроме 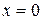 . Если степень
. Если степень 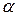 является четным отрицательным числом, то степенная функция является четной. В противном случае она является нечетной. Эти утверждения проиллюстрированы на рис. 3 и 4.
является четным отрицательным числом, то степенная функция является четной. В противном случае она является нечетной. Эти утверждения проиллюстрированы на рис. 3 и 4.
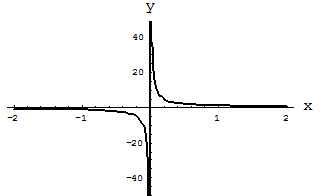
Рис. 3. Степенная функция 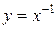
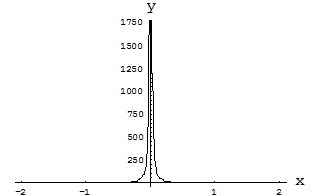
Рис. 4. Степенная функция 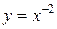
Среди степенных функций с показателем степени, являющимся рациональной дробью рассмотрим функцию 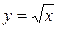 . Поскольку рассматривается арифметическое значение корня, то областью определения функции будет множество неотрицательных действительных чисел (
. Поскольку рассматривается арифметическое значение корня, то областью определения функции будет множество неотрицательных действительных чисел (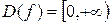 ). График этой степенной функции представлен на рис. 5.
). График этой степенной функции представлен на рис. 5.
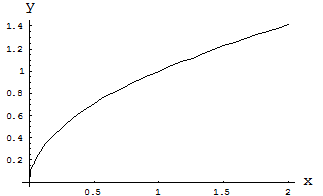
Рис. 5. Степенная функция 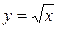
График функции 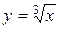 представлен на рис. 6. Областью определения функции является вся действительная ось.
представлен на рис. 6. Областью определения функции является вся действительная ось.
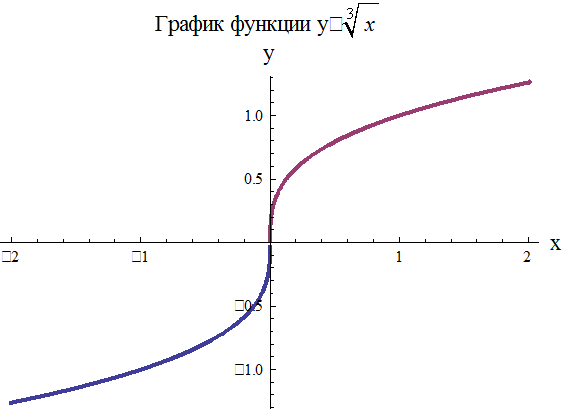
Рис. 6. Степенная функция 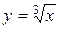
2.2. Показательная функция
Показательная функция задается следующим аналитическим выражением:
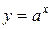 , (1)
, (1)
где 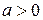 и
и 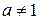 - действительное число.
- действительное число.
Показательная функция с указанными ограничениями для основания степени 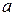 определена для любых значений
определена для любых значений 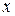 (
(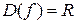 ). Вид показательной функции существенно зависит от основания степени
). Вид показательной функции существенно зависит от основания степени 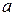 . Если
. Если 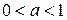 , то функция является убывающей (см. рис. 1). Если
, то функция является убывающей (см. рис. 1). Если 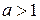 , то функция является возрастающей (см. рис. 2).
, то функция является возрастающей (см. рис. 2).
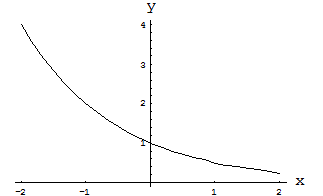
Рис. 1. Показательная функция 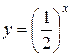 .
.
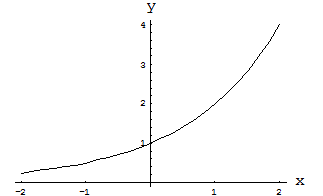
Рис. 2. Показательная функция 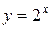 .
.
Отметим, что графики всех показательных функций проходят через одну и ту же точку с координатами 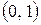 .
.
Логарифмическая функция задается следующим аналитическим выражением:
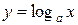 , (1)
, (1)
где 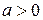 и
и 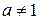 - действительное число. Она понимается как число, которое должно быть степенью числа
- действительное число. Она понимается как число, которое должно быть степенью числа 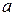 , чтобы получить
, чтобы получить 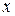 . Иначе говоря, значение функции должно быть таким, чтобы выполнялось соотношение
. Иначе говоря, значение функции должно быть таким, чтобы выполнялось соотношение
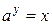 .
.
Число 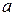 называется основанием логарифмической функции. Поскольку любая степень положительного числа дает также положительное число, то областью определения логарифмической функции (1) является множество положительных вещественных чисел (
называется основанием логарифмической функции. Поскольку любая степень положительного числа дает также положительное число, то областью определения логарифмической функции (1) является множество положительных вещественных чисел (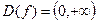 ). Вид логарифмической функции существенно зависит от величины основания логарифма
). Вид логарифмической функции существенно зависит от величины основания логарифма 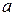 . Если
. Если 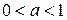 , то функция является убывающей (см. рис. 1). Если
, то функция является убывающей (см. рис. 1). Если 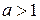 , то функция является возрастающей (см. рис. 2).
, то функция является возрастающей (см. рис. 2).
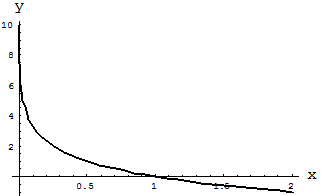
Рис. 1. Логарифмическая функция 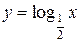 .
.
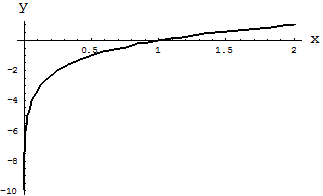
Рис. 2. Логарифмическая функция 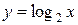 .
.
Отметим, что графики всех логарифмических функций проходят через одну и ту же точку с координатами 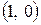 .
.
2.4. Тригонометрические функции
2.4.1. Функция 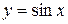
Аргумент 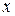 называется углом. Угол определяется как отношение длины дуги части окружности, проведенной из вершины угла как из центра, к величине радиуса окружности. Угол является безразмерной величиной. Однако условно его считают выраженным в радианах. Отметим, что угол может выражаться в градусах. Для острых углов, т. е. для углов величиной
называется углом. Угол определяется как отношение длины дуги части окружности, проведенной из вершины угла как из центра, к величине радиуса окружности. Угол является безразмерной величиной. Однако условно его считают выраженным в радианах. Отметим, что угол может выражаться в градусах. Для острых углов, т. е. для углов величиной 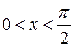 функция синуса определяется как отношение противолежащего катета к гипотенузе прямоугольного треугольника. Для остальных значений аргумента функция синуса определяется как ордината конца подвижного радиуса единичной окружности. Очевидно, что функция
функция синуса определяется как отношение противолежащего катета к гипотенузе прямоугольного треугольника. Для остальных значений аргумента функция синуса определяется как ордината конца подвижного радиуса единичной окружности. Очевидно, что функция 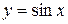 имеет период, равный
имеет период, равный 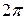 . График этой функции представлен на рис. 1.
. График этой функции представлен на рис. 1.
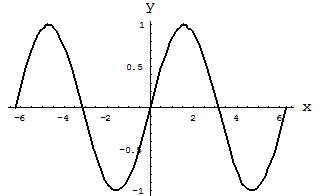
Рис. 1. Функция синуса 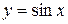 .
.
Областью определения функции синуса является все множество действительных чисел (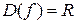 ).
).
2.4.2. Функция 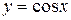
Для острых углов, т. е. для углов величиной 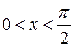 функция косинуса определяется как отношение прилежащего катета к гипотенузе прямоугольного треугольника. Для остальных значений аргумента функция косинуса определяется как абсцисса конца подвижного радиуса единичной окружности. Очевидно, что функция
функция косинуса определяется как отношение прилежащего катета к гипотенузе прямоугольного треугольника. Для остальных значений аргумента функция косинуса определяется как абсцисса конца подвижного радиуса единичной окружности. Очевидно, что функция 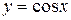 имеет период, равный
имеет период, равный 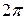 . График этой функции представлен на рис. 1.
. График этой функции представлен на рис. 1.
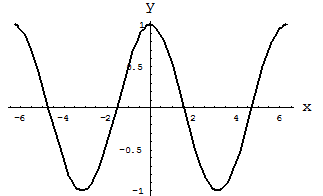
Рис. 1. Функция косинуса 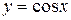 .
.
Областью определения функции косинуса является все множество действительных чисел (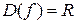 ).
).
2.4.3. Функция 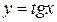
Для острых углов, т. е. для углов величиной 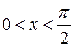 функция тангенса определяется как отношение противолежащего катета к прилежащему прямоугольного треугольника или как отношение синуса к косинусу
функция тангенса определяется как отношение противолежащего катета к прилежащему прямоугольного треугольника или как отношение синуса к косинусу
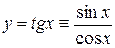 . (1)
. (1)
Для остальных значений аргумента функция тангенса определяется как отношение ординаты конца подвижного радиуса единичной окружности к его абсциссе или как ордината точки пересечения подвижного луча с прямой перпендикулярной оси абсцисс и проходящей через точку с координатами 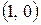 . Функция
. Функция 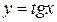 имеет период, равный
имеет период, равный 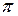 . График этой функции представлен на рис. 1.
. График этой функции представлен на рис. 1.
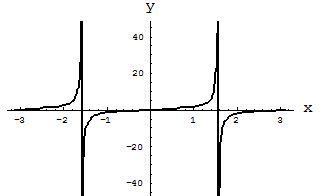
Рис. 1. Функция тангенса 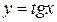 .
.
Областью определения функции косинуса является все множество действительных чисел кроме тех, в которых функция косинуса обращается в нуль, т. е. кроме
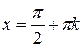 ,
,
где 
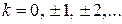 (
(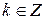 ).
).
2.4.4. Функция 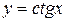
Для острых углов, т. е. для углов величиной 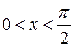 функция котангенса определяется как отношение прилежащему катета противолежащего к прямоугольного треугольника или как отношение косинуса к синусу
функция котангенса определяется как отношение прилежащему катета противолежащего к прямоугольного треугольника или как отношение косинуса к синусу
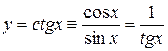 . (1)
. (1)
Для остальных значений аргумента функция тангенса определяется как отношение абсциссы конца подвижного радиуса единичной окружности к его ординате или как абсцисса точки пересечения подвижного луча с прямой перпендикулярной оси ординат и проходящей через точку с координатами 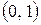 . Функция
. Функция 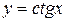 имеет период, равный
имеет период, равный 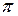 . График этой функции представлен на рис. 1.
. График этой функции представлен на рис. 1.
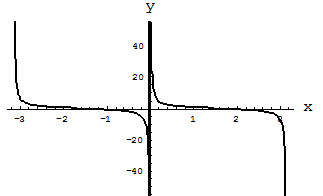
Рис. 1. Функция тангенса 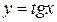 .
.
Областью определения функции котангенса является все множество действительных чисел кроме тех, в которых функция синуса обращается в нуль, т. е. кроме
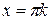 ,
,
где 
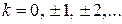 (
(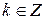 ).
).
2.5. Обратные тригонометрические функции
2.5.1. Функция 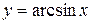
Величина 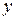 называется углом. Величина
называется углом. Величина 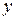 определяется равенством
определяется равенством
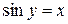 . (1)
. (1)
Поскольку функция синуса является периодической, то соотношению (1) удовлетворяет множество значений 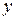 . Среди всевозможных значений функции (1) выбирают только те, которые попадают в интервал
. Среди всевозможных значений функции (1) выбирают только те, которые попадают в интервал
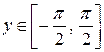 .
.
Последний и составляет область изменения функции 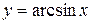 (
(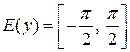 ). Поскольку значение функции (1) по модулю не превосходит единице, то областью определения функции
). Поскольку значение функции (1) по модулю не превосходит единице, то областью определения функции 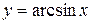 является
является 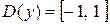 .
.
График этой функции представлен на рис. 1.
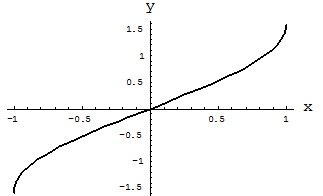
Рис. 1. Функция арксинуса 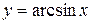 .
.
2.5.2. Функция 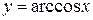
Величина 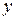 называется углом. Величина
называется углом. Величина 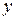 определяется равенством
определяется равенством
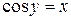 . (1)
. (1)
Поскольку функция косинуса является периодической, то соотношению (1) удовлетворяет множество значений 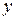 . Среди всевозможных значений функции (1) выбирают только те, которые попадают в интервал
. Среди всевозможных значений функции (1) выбирают только те, которые попадают в интервал
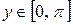 .
.
Последний и составляет область изменения функции 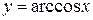 (
(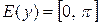 ). Поскольку значение функции (1) по модулю не превосходит единице, то областью определения функции
). Поскольку значение функции (1) по модулю не превосходит единице, то областью определения функции 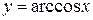 является
является 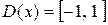 .
.
График этой функции представлен на рис. 1.
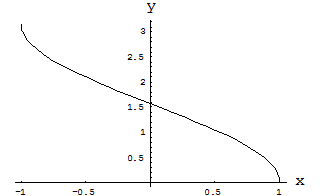
Рис. 1. Функция арккосинуса 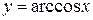 .
.
2.5.3. Функция 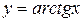
Величина 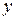 называется углом. Величина
называется углом. Величина 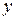 определяется равенством
определяется равенством
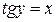 . (1)
. (1)
Поскольку функция тангенса является периодической, то соотношению (1) удовлетворяет множество значений 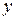 . Среди всевозможных значений функции (1) выбирают только те, которые попадают в интервал
. Среди всевозможных значений функции (1) выбирают только те, которые попадают в интервал
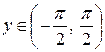 .
.
Последний и составляет область изменения функции 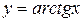 (
(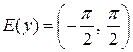 ). Поскольку функция (1) может принимать любое действительное значение, то областью определения функции
). Поскольку функция (1) может принимать любое действительное значение, то областью определения функции 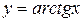 является
является 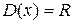 .
.
График этой функции представлен на рис. 1.
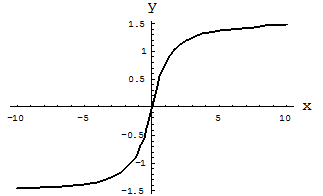
Рис. 1. Функция арктангенса 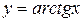 .
.
2.5.4. Функция 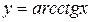
Величина 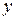 называется углом. Величина
называется углом. Величина 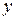 определяется равенством
определяется равенством
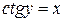 . (1)
. (1)
Поскольку функция котангенса является периодической, то соотношению (1) удовлетворяет множество значений 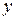 . Среди всевозможных значений функции (1) выбирают только те, которые попадают в интервал
. Среди всевозможных значений функции (1) выбирают только те, которые попадают в интервал
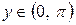 .
.
Последний и составляет область изменения функции 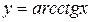 (
(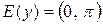 ). Поскольку функция (1) может принимать любое действительное значение, то областью определения функции
). Поскольку функция (1) может принимать любое действительное значение, то областью определения функции 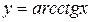 является
является 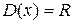 .
.
График этой функции представлен на рис. 1.
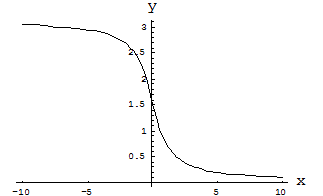
Рис. 1. Функция арккотангенса 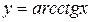 .
.
[1] В учебнике Шнейдера В. Е. и др. «Краткий курс высшей математики. Т. 1» к основным элементарным функциям относят постоянную.
[2]В учебнике Шнейдера В. Е. и др. «Краткий курс высшей математики. Т. 1» добавлено «не равное нулю».
 2015-08-21
2015-08-21 9142
9142