Простые, сложные и непрерывно начисляемые проценты

При многократном начислении простых процентов начисление делается по отношению к исходной сумме и представляет собой каждый раз одну и ту же величину. Иначе говоря,

,

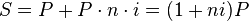где

· P — исходная сумма

· S — наращенная сумма (исходная сумма вместе с начисленными процентами)

· i — процентная ставка, выраженная в долях за период

· n — число периодов начисления

В этом случае говорят о простой процентной ставке.

При многократном начислении сложных процентов начисление каждый раз делается по отношению к сумме с уже начисленными ранее процентами. Иначе говоря,

S = (1 + i) ⁿP

(при тех же обозначениях).

В этом случае говорят о сложной процентной ставке.

Часто рассматривается следующая ситуация. Годовая процентная ставка составляет j, а проценты начисляются m раз в году по сложной процентной ставке равной j / m (например, поквартально, тогда m = 4 или ежемесячно, тогда m = 12). Тогда формула для наращенной суммы через k лет:

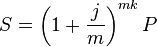
В этом случае говорят о номинальной процентной ставке. Сравнение сложных процентных ставок с разными интервалами начисления производят при помощи показателя годовая процентная доходность(APY).

Наконец, иногда рассматривают ситуацию так называемых непрерывно начисляемых процентов, то есть годовое число периодов начисления m устремляют к бесконечности. Процентную ставку обозначают δ, а формула для наращенной суммы:

S = e ^{δ n} P.

В этом случае номинальную процентную ставку δ называют сила роста.