2015-08-21
14673
Уравнение того же вида, что и уравнение (7-5), может быть использовано для определения потерь напора на трение также при турбулентном движении жидкости. Однако выражение для коэффициента трения в данном случае не может быть выведено теоретически из-за сложности структуры турбулентного потока и невозможности решения для него уравнений Навье–Стокса. Поэтому расчетные уравнения для определения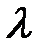 
при турбулентном движении получают обобщением результатов экспериментов методом теории подобия.
Представим обобщенное уравнение в степенной форме:
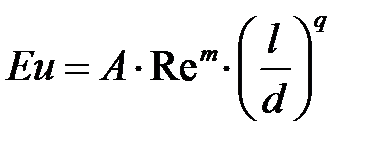
В результате обобщения опытных данных, полученных при движении жидкостей в трубопроводах с гладкими стенками в пределах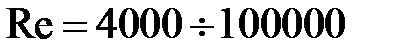 
, найдены следующие числовые значения коэффициента А и показателей степеней: 
.
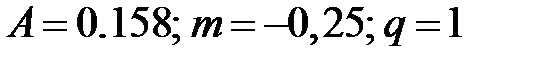Следовательно, расчетное уравнение принимает вид
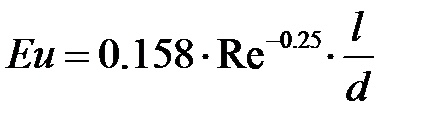
При подстановке в это уравнение выражения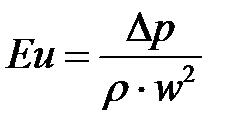 
(с учетом того, что 
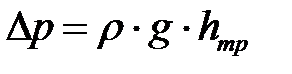) получим
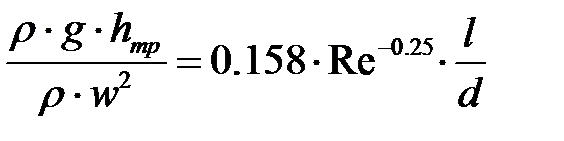
или после элементарных преобразований
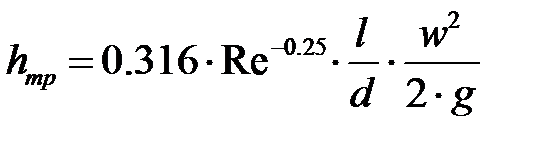| 8-6 |
Сопоставление уравнения (8-5) с уравнением (8-7) показывает, что при турбулентном движении в гладких трубах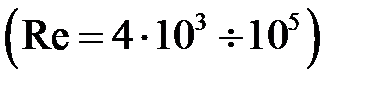 
коэффициент трения выражается обобщенной зависимостью
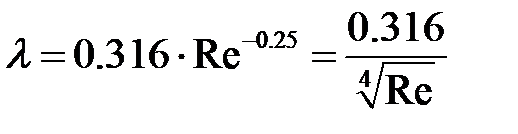| 8-7 |
Таким образом, если при ламинарном движении потеря напора на трение пропорциональна скорости жидкости в первой степени [см. уравнение (8-2)], то при турбулентном движении эта потеря напора в большей мере зависит от скорости – потерянный напор пропорционален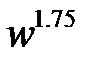 
.
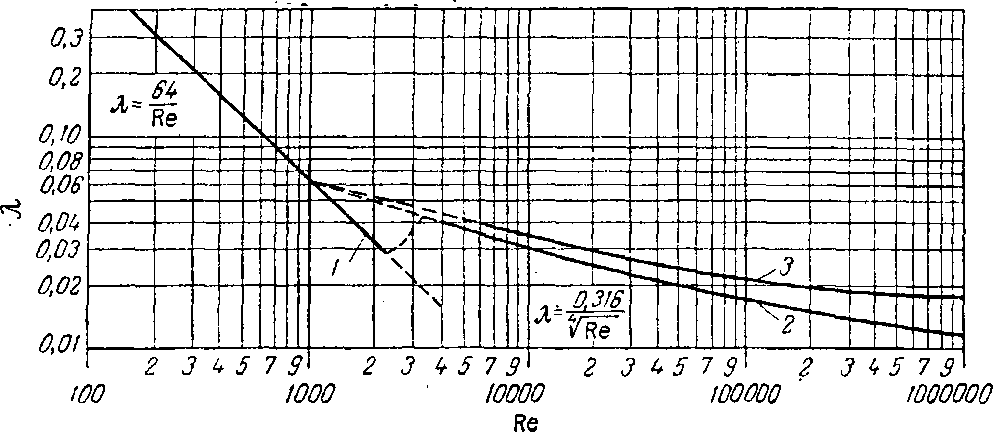
Рис. 8-1. Зависимость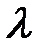 
, от критерия Re
1 – гладкие и шероховатые трубы; 2 – гладкие трубы (медь, латунь, свинец, стекло); 3 – шероховатые трубы (сталь, чугун).
При турбулентном потоке коэффициент трения в общем случае зависит не только от характера движения жидкости (значения Re), но и от шероховатости стенок труб. Из рис. 8-1 видно, что при турбулентном режиме значения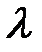 
, для негладких труб выше, чем следует из уравнения (8-7). На рисунке показано, что в небольшой области вблизи критического значения Re режим движения является неустойчивым и величину 
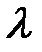надежно определить нельзя.
Шероховатость труб может быть количественно оценена некоторой усредненной величиной абсолютной шероховатости 
, представляющей собой среднюю высоту выступов шероховатости на внутренней поверхности труб. По опытным данным, для новых стальных труб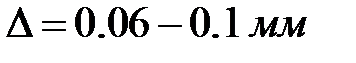 
; для бывших в эксплуатации, но не сильно подвергнутых действию коррозии стальных труб 
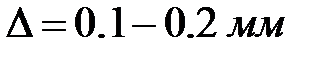, для старых загрязненных стальных и чугунных труб 
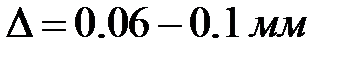и т. д.
Влияние шероховатости на величину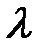 
, определяется соотношением между средней высотой выступов шероховатости 
и толщиной вязкого подслоя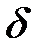 
, движение жидкости в котором можно считать практически ламинарным. В некоторой начальной области турбулентного движения, когда толщина вязкого подслоя больше высоты выступов шероховатости (
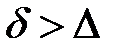), жидкость плавно обтекает эти выступы и влиянием шероховатости на величину 
, можно пренебречь. В указанной области турбулентного движения трубы можно рассматривать как гидравлически гладкие и вычислять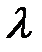 
по уравнению (8-7).
При возрастании Re величина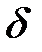 
уменьшается. Когда она становится сравнимой с абсолютной шероховатостью (
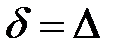) и меньше ее (
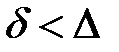), вязкий подслой уже не покрывает выступов шероховатости. В таких условиях коэффициент трения все больше начинает зависеть от шероховатости. При этом величина 
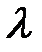, а следовательно, и потеря напора на трение возрастают под действием сил инерции, возникающих вследствие дополнительного вихреобразования вокруг выступов шероховатости.
Таким образом, с увеличением критерия Рейнольдса зона гладкого трения, в которой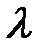 
зависит лишь от Re, переходит сначала в зону смешанного трения, когда на величину 
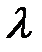влияют и Re и шероховатость, а затем в автомодельную (по отношению к Re) зону, когда величина 
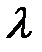, практически перестает зависеть от критерия Рейнольдса и определяется лишь шероховатостью стенок труб (8-2).
Автомодельную область называют также областью квадратичного закона сопротивления при отсутствии влияния Re (т.е. скорости) на величину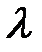 
, сопротивление трения становится пропорциональным квадрату скорости.
Re
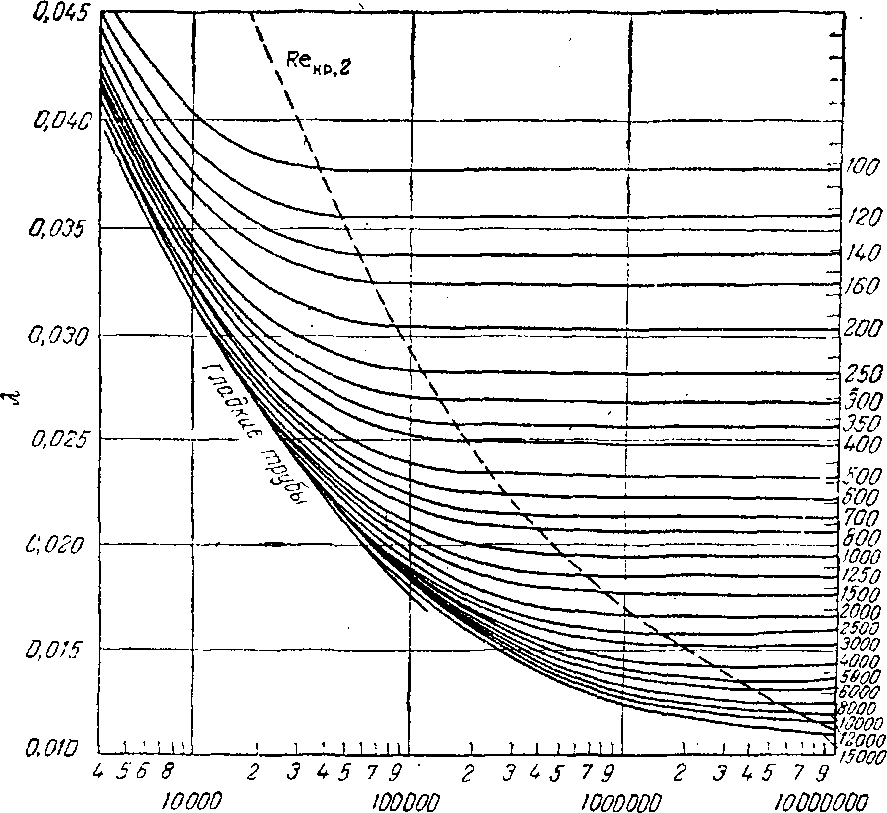
Рис. 8-2. Зависимость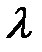 
от критерия Re при различных относительных шероховатостях.
Критические значения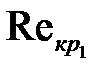 
, при которых шероховатость начинает влиять на коэффициент трения, а также критические значения 
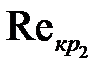, при которых 
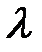становится функцией только шероховатости трубы (см. пунктир на рис. 8-2), зависят от относительной шероховатости 
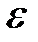, выражаемой отношением абсолютной шероховатости 
к диаметру d трубы:
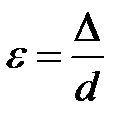| 8-8 |
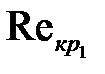и 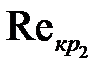ориентировочно определяют по уравнениям:
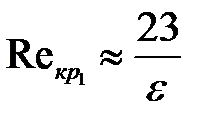| 8-9 |
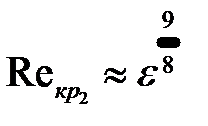| 8-9а |
При расчете коэффициента трения для всех областей (зон) турбулентного движения применимо общее уравнение
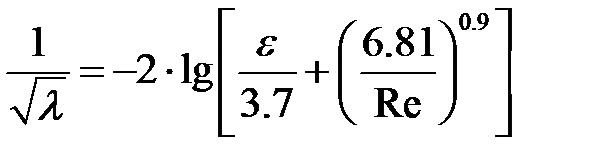| 8-10 |
Для области гладкого трения расчет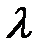 
производят по уравнению (8-7) или по уравнению (8-10), из которого исключено первое слагаемое в квадратных скобках. Этот член отражает влияние шероховатости и является для данной зоны пренебрежимо малой величиной. Соответственно
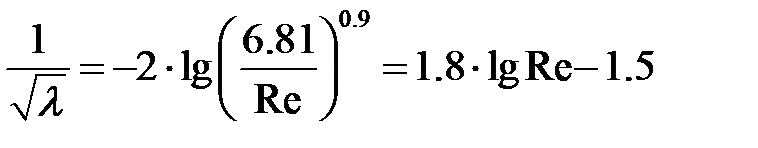| 8-10 |
Для автомодельной области, когда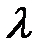 
перестает зависеть от Re, в уравнении (810) можно пренебречь вторым слагаемым в квадратных скобках, и оно принимает вид
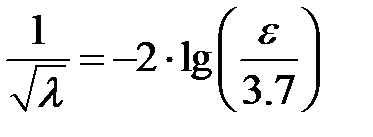| 8-11 |
В случае движения газов по трубопроводам большой протяженности при расчете необходимо учитывать изменения плотности газа из-за уменьшения давления (в результате потери напора) по длине трубы. Если движение газа при этом сопровождается значительным изменением температуры по длине трубопровода, то нужно учитывать изменение плотности газа и вследствие изменения температуры.
Приведенные расчетные уравнения получены для изотермических условий течения жидкости. При нагревании или охлаждении движущейся жидкости через стенки трубы в результате изменения температуры меняется и вязкость жидкости по сечению трубы. Это вызывает некоторое изменение профиля скоростей по данному сечению и, соответственно, изменение величины 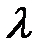. Особенно существенно влияние теплообмена на величину 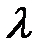при ламинарном режиме течения, когда поперечное перемешивание жидкости отсутствует и градиент температуры по поперечному сечению трубы в основной массе жидкости значительно выше, чем в турбулентном потоке.
Поэтому, если средняя температура потока значительно отличается от температуры стенки трубы, во все рассмотренные выше уравнения для расчета 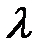[исключая уравнение (8-11) для автомодельной области, где 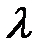не зависит от Re] следует вводить поправочные множители, которые находят по специальным формулам, приводимым в справочной литературе.
