Вероятностные модели механизма старения информации

Интенсивность старения информации выражается в виде той части еще не учтенной полезной информации, которая может быть использована в прогнозной моде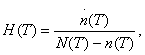ли:

или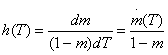

где

m(T), которая обозначает долю полезной информации в общем ее объеме;

п(Т) - глубина ретроспекции, выраженная в "квантах ин­формации" и использованная в модели, на момент времени Т;

N(Т) - нижняя граница сферы распространения полезной информации, выраженная в тех же единицах.

Под “ квантом информации ” будем понимать некоторый элемент, который может восприниматься и использоваться са­мостоятельно.

Глубина ретроспекции – период времени в прошлом, по которому имеется необходимая и достаточная информация об объекте.

Кумуляция информации – это ее систематизация, оценка и обобщение.

Интенсивность старения информации H(T) и h(T) определяет конкретную конфигурацию кривой h(T) или m(T).

Отсюда следует, что дифференциальное уравнение кумуляции информации имеет вид:

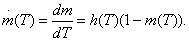
Интенсивность старения информации в общем случае будет зависеть от самых различных факторов. Поэтому функция h(t) можно записать в следующем общем виде

h(T)=h(T,m(T),xi)

где xi – множество экзогенных факторов, определяющих конкретный процесс старения информации.

Здесь предполагается, что значения этих факторов явно не зависят от m(T), T. Дальнейший анализ динамики процесса старения информации состоит в спецификации вида функции h, который необходимо проводить исходя из эмпирических соображений.

Для выявления тенденций использования информации в исследованиях получило распространение аналитическое выравнивание эмпирических рядов распределения с помощью различных функций, которые описывают полиномы и комуляты распределения квантов информации, получаемые при наблюдении.

Интенсивность старения ин­формации будет определяться двумя составляющими: константой а, не зависящей от длительности жизненного цикла полезной информации, и слагаемым, экспоненциального растущим со временем

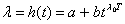
Эта функция, постоянные которой а, b и 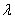определяются статистическим путем на основе известных алгоритмов (методом трех сумм, методом трех точек и др.) имеет горизонтальную асимптоту, равную а. Ее график стремится к асимптоте при 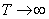, но никогда ее не пересекает. Параметр b равен разности между ординатой кривой (при 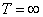) и асимптотой. Тогда, подставляя выражение (2.11) в зависимость (2.6) после очевидных преобразований, можно получить

.

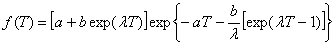Вероятностные модели механизма старения информации

Общий способ построения широкого класса вероятностных моделей старения информации при рандомизации параметра 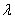и использовании аппарата характеристических функций рассмотрим на следующем примере, имеющем прикладное значение. Так, например, если маргинальное (частное) распределение параметра Т₀ в свою очередь имеет плотность

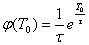
(случайный характер параметра Т₀ может быть обусловлен нарушением стационарности процесса, неоднородностью ретроспективного ряда значений Т₀, ограниченным объемом информации и др.), то характеристическая функция безусловного распределения случайной величины Т₀ будет иметь вид

,

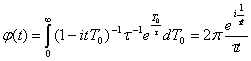где 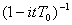- характеристическая функция экспоненциаль­ного распределения. С помощью формулы обращения, плотность распределения случайной величины Т определяется следующим образом

,

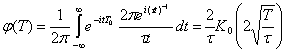где 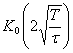- модифицированная функция Бесселя третьего порядка.

На продолжительность существования полезной для про­гноза информации оказывает влияние колебание (изменение) цен на товары и услуги, динамика бюджета потребителя, изменение объема спроса на товар и других в общем случаеограниченного числа факторов.

В связи с этим представляется целесообразным при формировании математической модели старения информации использовать теоретико-вероятностную схему формирования законов распределения показателей как сумм не­большого случайного числа случайных величин.

Решение практических задач анализа и прогнозирования времени существования полезной информации в микроэкономике требует применения методов построения непредельных распределений сумм случайного числа случайных величин, нахождения их квантильных функций и оценки с их помощью предпрогнозного фона.

Основываясь на свойствах характеристической функции

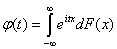
и используя ее основные свойства, приведем некоторые результаты, касающиеся законов распределения для сумм

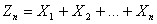
n первых случайных величин из бесконечной последовательности

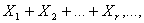
где само число слагаемых n есть случайная величина. В дальнейшем r будем обозначать случайную величину, способную принимать неотрицательные значения в зависимости от схематизации стохастического эксперимента

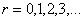
Вероятность события заключающуюся в том, что 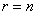, обозначим

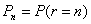
Кроме того будем предполагать, что случайные величины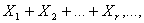

независимы, одинаково распределены и независимы от случайной величины п.

Будем также предполагать существование математических ожидани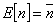й

и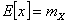

Функция распределения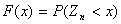

суммы случайного числа n случайных величин Х_i, на основании мультипликативного свойства характеристической функции определяется характе­ристической функцией

,

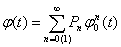где 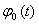характеристическая функция случайной величины Х.

С помощью формулы обращения запишем формулу для плотности распределения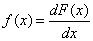

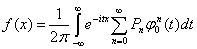
Конечность выражения

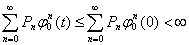
гарантирует замену порядка суммирования и интегрирования, следовательно

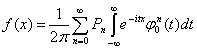
В силу мультипликативности свойства функции и теоремы единственности

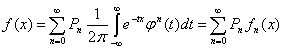
где 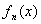- плотность распределения сумм n случайных величин X_i/

Таким образом, плотность непредельного распределения случайного числа случайных величин представляет собой смесь распределений с плотностью f_n (x) вероятность появления ко­торых в случайной выборке (удельный вес наблюдений в общей генеральной совокупности) равна Р_n.

Следует заметить, что та­кого рода комбинации распределений удобны в методологиче­ском плане и могут найти применение в прикладной стати­стике при анализе генеральных совокупностей, объединяю­щих в себе несколько подсовокупностей, каждая из которых, в определенном смысле, однородна и описывается основным мо­дельным распределением, например, нормальным, экспо­ненциальным и т.д. В рассматриваемой проблеме подсовокупности могут описывать статистику промежутков между кванта­ми информации.

В качестве примера рассмотрим распределение суммы пуассоновского числа стандартных нормальных величин.

Характеристическая функция стандартного нормального распределения

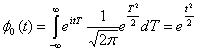
Отсюда характеристическая функция распределения суммы пуассоновского числа стандартных нормальных величин имеет вид

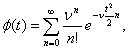
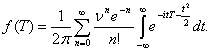
В результате интегрирования получим

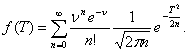
Полученная плотность распределения претерпевает значительную деформацию по сравнению с предельным нормальным распределением. Сумма случайного числа случайных величин, как видно из формулы, распределена по закону, отлично­го от нормального, и это отличие тем существенней, чем больше удельный вес имеют вероятности получения малых значений случайных чисел п. Это обстоятельство имеет весьма важное значение для решения вопроса отбраковки устаревшей информации.

К аналогичному выводу можно прийти, рассматривая сумму пуассоновского числа экспоненциально распределенных слу­чайных величин. В этом случае плотность распределения имеет вид

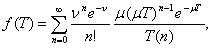
где m – величина, обратная среднему значению случайной величины Т.

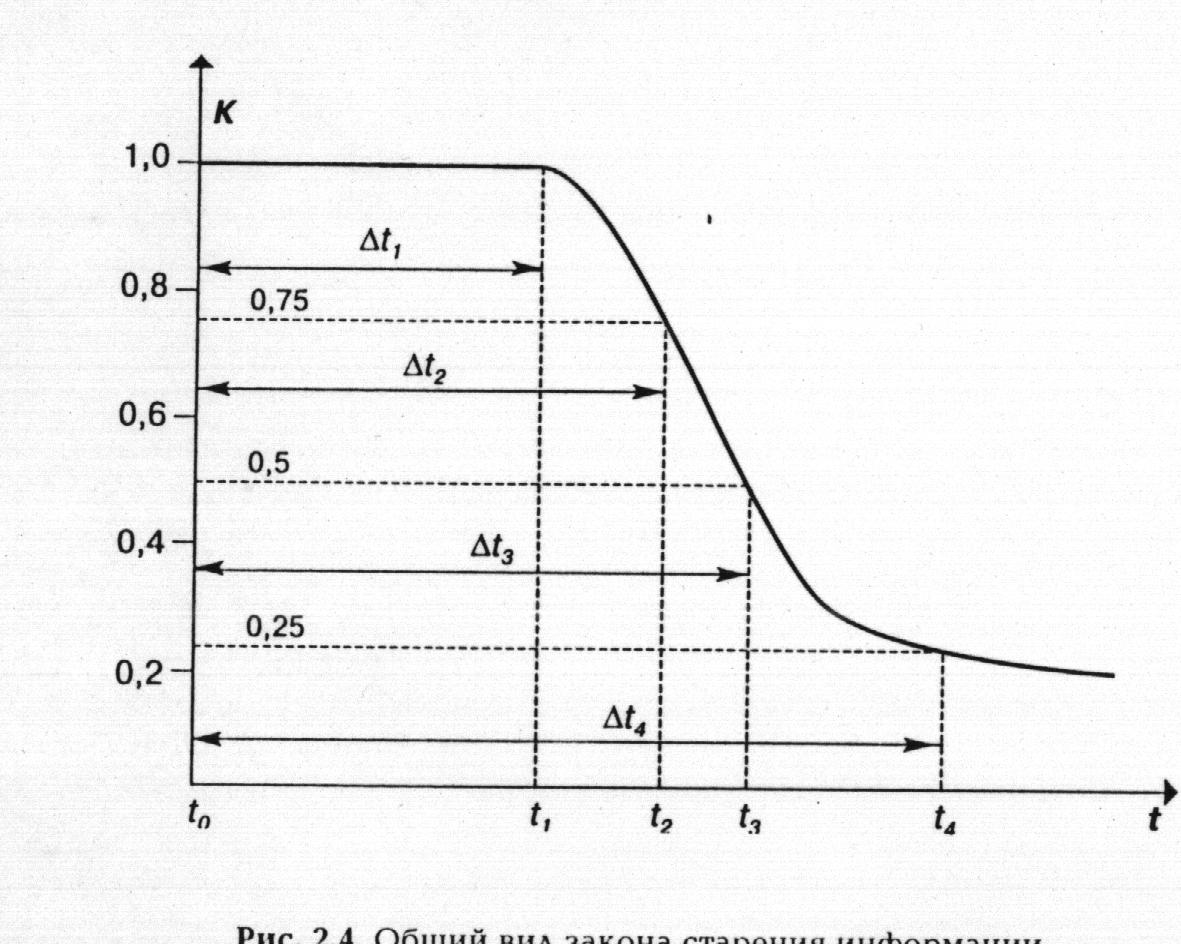
Закон старения информации

Список литературы.

1. 1. Ефимов А.Н. Информация, ценность, старение, рассеяние. – М.: Знание, 1978. – 64 с.

2. Дворянкин С. В., Минаев В.А., Никитин М. М., Скрыль С. В., Фисун А. П. Правовое обеспечение информационной безопасности. 2008 г.

3. Б.П Ивченко, Л.А. Мартыщенко, И.Б. Иванцов. «Информационная микроэкономика». Часть 1. Методы анализа и прогнозирования, СПб.: «Нордмед-Издат», 1997. – 160 с

4. МОДЕЛЬ ВЗАИМОСВЯЗИ ЦЕННОСТИ И СТАРЕНИЯ ИНФОРМАЦИИ. Л.М. Виткин, В.У. Игнаткин. 2007 г.