1. Доказать, что у выпуклого многоугольника каждый угол меньше 1800.
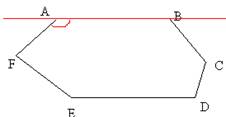 | Дано: мног-к ABCDEF. Доказать:  FAB< 1800. Доказательство: Возьмем любой угол многоугольника ABCDEF, например, FAB< 1800. Доказательство: Возьмем любой угол многоугольника ABCDEF, например,  FAB и его сторону ВА, выходящую из вершины А. Т.к. многоугольник выпуклый, то он лежит по одну сторону от прямой АВ. Значит и его угол лежит по одну сторону от прямой АВ. Значит, FAB и его сторону ВА, выходящую из вершины А. Т.к. многоугольник выпуклый, то он лежит по одну сторону от прямой АВ. Значит и его угол лежит по одну сторону от прямой АВ. Значит,  FAB меньше развернутого, т.е. FAB меньше развернутого, т.е.  FAB< 1800. FAB< 1800. |
2. Сколько сторон имеет правильный многоугольник, каждый из внутренних углов которого равен 1350?
Решение: Сумма внутренних углов многоугольника определяется формулой 1800(n - 2), где n- число сторон. По условию задачи имеем: 135n=180(n-2). 135n-180n+360=0. Отсюда n=8. Ответ: 8.
3. В окружность вписан одиннадцатиугольник, одна из сторон которого равна радиусу окружности, а остальные десять равны между собой. Найдите углы одиннадцатиугольника.
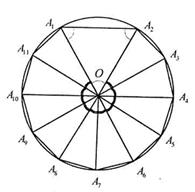 | Дано: A1А2А3 … А10А11- одиннадцатиугольник, вписанный в окружность (О, ОА1). А1А2=ОА1; А2А3=А3А4=…=А10А11=А11А1. Найти:  А1А2А3, А1А2А3,  А2А3А4, А2А3А4,  А3А4А5,… А3А4А5,…  А10А11А1, А10А11А1,  А11А1А2. Решение: Рассмотрим А11А1А2. Решение: Рассмотрим 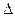 ОА1А2: А1А2=ОА1 = ОА2, ОА1А2: А1А2=ОА1 = ОА2,  А1ОА2=600. Т.к. А2А3=А3А4=…=А10А11=А11А1 и ОА1=ОА2=… ОА10=ОА11, то А1ОА2=600. Т.к. А2А3=А3А4=…=А10А11=А11А1 и ОА1=ОА2=… ОА10=ОА11, то 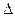 ОА2А3 = ОА2А3 = 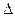 ОА3А4 = …= ОА3А4 = …= 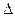 ОА10А11 = ОА10А11 = 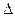 ОА11А1. ОА11А1.  А2ОА3= А2ОА3=  А3ОА4=…= А3ОА4=…=  А10ОА11= А10ОА11=  А11ОА1= А11ОА1= 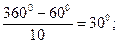  ОА2А3= ОА2А3=  А3А2О= А3А2О=  ОА3А4= ОА3А4=  А4А3О=…= А4А3О=…=  ОА11А1= ОА11А1=  А1А11О= А1А11О= 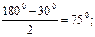  А11А1А2= А11А1А2=  А1А2А3=600+750=1350. А1А2А3=600+750=1350.  А2А3А4= А2А3А4=  А3А4А5=…= А3А4А5=…=  А9А10А11= А9А10А11=  А10А11А1=750+750=1500. Ответ: 300, 750, 1500. А10А11А1=750+750=1500. Ответ: 300, 750, 1500. |
4. Стороны выпуклого пятиугольника в котором все внутренние углы тупые, продолжили до взаимного пересечения. Вычислите сумму углов при вершинах полученной пятиугольной звезды.
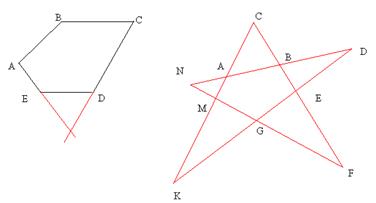 | Дано: ABCDE выпуклый пятиугольник. Найти сумму углов при вершинах полученной пятиугольной звезды. Решение:  АВС+ АВС+  ВСА+ ВСА+  САВ=1800. Отсюда САВ=1800. Отсюда  С=1800-( С=1800-( САВ+ САВ+  АВС). Выразив таким образом каждый угол при вершинах звезды, получим, что их сумма равна разности между 1800∙5 и удвоенной суммой внешних углов многоугольника, т.е. 1800∙5-3600∙2=1800. Ответ: 1800. АВС). Выразив таким образом каждый угол при вершинах звезды, получим, что их сумма равна разности между 1800∙5 и удвоенной суммой внешних углов многоугольника, т.е. 1800∙5-3600∙2=1800. Ответ: 1800. |
5. Точка F лежит на стороне АВ правильного восьмиугольника ABCDMNPQ так, что AF= 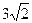 , FB=
, FB= 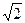 . Найдите расстояние от точки F до прямых, содержащих стороны восьмиугольника.
. Найдите расстояние от точки F до прямых, содержащих стороны восьмиугольника.
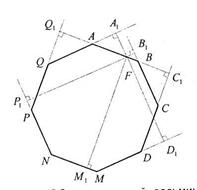 | Дано: ABCDMNPQ – правильный восьмиугольник, F 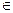 AB, AF=3 AB, AF=3 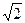 , BF= , BF= 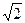 . найти: FA1, FB1, FC1, FD1, FM1, FP1, FQ1. Решение: 1) Рассмотрим . найти: FA1, FB1, FC1, FD1, FM1, FP1, FQ1. Решение: 1) Рассмотрим 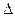 AА1F, он прямоугольный равнобедренный, т.к. AА1F, он прямоугольный равнобедренный, т.к.  QAB=1350 и QAB=1350 и  AA1F=900, AA1F=900,  A1AF = A1AF =  A1FA =450. 2) Из A1FA =450. 2) Из 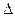 АА1F: FA1=AFcos450=3 АА1F: FA1=AFcos450=3 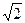 ∙ ∙ 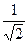 =3. Сторона восьмиугольника составляет: а=AF+FB=3 =3. Сторона восьмиугольника составляет: а=AF+FB=3 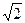 + + 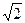 =4 =4 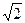 . Из рисунка следует: A1D1=AD=BC+(AB+CD)cos450, A1D1=8+4 . Из рисунка следует: A1D1=AD=BC+(AB+CD)cos450, A1D1=8+4 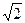 ; FD1=A1D1-FA1=5+4 ; FD1=A1D1-FA1=5+4 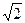 . 3) Из . 3) Из 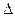 FB1B: FB1=FB∙cos450= FB1B: FB1=FB∙cos450= 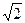 ∙ ∙ 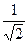 =1; FP1=BP-FB1=7+ 4 =1; FP1=BP-FB1=7+ 4 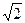 . 4) Рассмотрим . 4) Рассмотрим 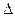 QQ1A, он – равнобедренный прямоугольный. Q1A=QA∙cos450=4 QQ1A, он – равнобедренный прямоугольный. Q1A=QA∙cos450=4 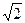 ∙ ∙ 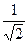 =4. FQ1=FA+Q1A=4+3 =4. FQ1=FA+Q1A=4+3 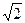 , FC1=FB+BC1=4+ , FC1=FB+BC1=4+ 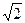 . Ответ: 3, 1, 4+ . Ответ: 3, 1, 4+ 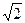 , 5+4 , 5+4 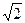 , 8+4 , 8+4 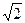 , 7+ 4 , 7+ 4 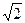 , 4+3 , 4+3 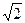 . . |
6. Может ли n – угольник иметь ровно 10 диагоналей?
Решение: 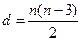 . d=10. Отсюда
. d=10. Отсюда 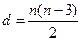 =10. n(n-3)=20. n2-3n-20=0. D=9+80=89.Т.е. целых корней нет. Следовательно, не может.
=10. n(n-3)=20. n2-3n-20=0. D=9+80=89.Т.е. целых корней нет. Следовательно, не может.
7. Диагонали трапеции делят углы, прилежащие к большему основанию, пополам. Периметр трапеции равен 36 м, а средняя линия 11,7 м. Найдите стороны трапеции.
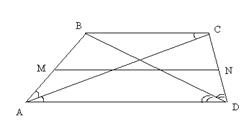 | Дано: ABCD - трапеция.  ВАС= ВАС=  САD, САD,  CDB= CDB=  ВDA, P=36 м, MN=11,7. Найти: АВ, ВС, CD, AD. Решение: 1) P=AB+BC+CD+AD=36. MN= ВDA, P=36 м, MN=11,7. Найти: АВ, ВС, CD, AD. Решение: 1) P=AB+BC+CD+AD=36. MN= 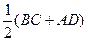 . Отсюда BC+AD=2MN=23,4. AB+CD+23,4=36. AB+CD=12,6. 2) Т.к. BC||AD и АС – секущая, то . Отсюда BC+AD=2MN=23,4. AB+CD+23,4=36. AB+CD=12,6. 2) Т.к. BC||AD и АС – секущая, то  CAD= CAD=  BCA – внутренние накрест лежащие, и следовательно, BCA – внутренние накрест лежащие, и следовательно, 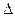 АВС – равнобедренный, а значит, АВ=ВС. 3) Аналогично, АВС – равнобедренный, а значит, АВ=ВС. 3) Аналогично, 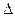 BCD – равнобедренный и BC=CD. 4) Обозначим ВС=х, AD=y, получим BCD – равнобедренный и BC=CD. 4) Обозначим ВС=х, AD=y, получим 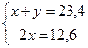 . Отсюда х=6,3, у=17,1. Ответ: 6,3; 6,3; 6,3; 17,1. . Отсюда х=6,3, у=17,1. Ответ: 6,3; 6,3; 6,3; 17,1. |
8. В равнобокой трапеции большее основание равно 3,7 см, боковая сторона равна 1,5 см, а угол между ними равен 600. Найдите среднюю линию трапеции.
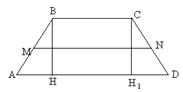 | Дано: ABCD - трапеция. AD=3,7, AB=CD=1,5.  ВАD=600. Найти: MN. Решение: 1) MN= ВАD=600. Найти: MN. Решение: 1) MN= 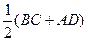 = = 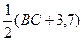 . 2) В . 2) В 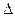 ABH: ABH:  ABH=300, отсюда AH= ABH=300, отсюда AH=  AB, HH1=BC=3,7=1,5=2,2. MN= AB, HH1=BC=3,7=1,5=2,2. MN=  (2,2+3,7)=2,95. Ответ: 2,95. (2,2+3,7)=2,95. Ответ: 2,95. |
9. Основания трапеции равны 4 и 3, а боковые стороны при продолжении пересекаются под прямым углом. Найдите длину отрезка, соединяющего середины оснований трапеции.
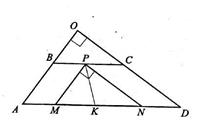 | Дано: ABCD - трапеция. О=АВ 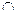 CD, CD,  O=900. BC=3, AD=4. Найти: PK. Решение: 1) ВР = PC, АК=KD – по условию, O=900. BC=3, AD=4. Найти: PK. Решение: 1) ВР = PC, АК=KD – по условию,  AOD= 90°. Проведем МР||АВ, PN || CD, тогда AOD= 90°. Проведем МР||АВ, PN || CD, тогда  MPN= 90° (как угол между соответственно параллельными прямыми), ВР = AM =1,5; PC = ND= 1,5 (как противоположные стороны параллелограмма). Тогда AM =ND=1 ,5, а MK=KN=0,5. 2) Отрезок РК — это медиана прямоугольного треугольника MNP. По свойству медианы прямоугольного треугольника будем иметь РК = 0,5. (Медиана равна гипотенузе). MPN= 90° (как угол между соответственно параллельными прямыми), ВР = AM =1,5; PC = ND= 1,5 (как противоположные стороны параллелограмма). Тогда AM =ND=1 ,5, а MK=KN=0,5. 2) Отрезок РК — это медиана прямоугольного треугольника MNP. По свойству медианы прямоугольного треугольника будем иметь РК = 0,5. (Медиана равна гипотенузе). |
10. Основания трапеции относятся как 2:3, а средняя линия равна 5 м. Найдите основания трапеции.
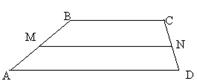 | Дано: ABCD - трапеция. BC:AD=2:3. MN=5. Найти: BC, AD. Решение: 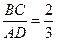 , MN= , MN= 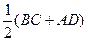 . Обозначим ВС=х, AD=y, тогда получим систему: . Обозначим ВС=х, AD=y, тогда получим систему: 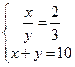 . Отсюда, ответ: 4 и 6. . Отсюда, ответ: 4 и 6. |
11. Средняя линия трапеции равна 2,4 м и делится диагональю на два отрезка, разность которых равна 0,6 м. Найдите основания данной трапеции.
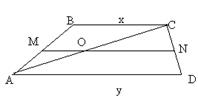 | Дано: ABCD - трапеция. MN=2,4 см. МО-ОN=0,6. Найти: BC, AD. Решение: 1) MN= 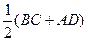 . Обозначим ВС=х, AD=y, тогда х+у=4,8. МО-ОN=0,6, МО+ОN=2,4. Тогда 2МО=3, МО=1,5. ON=2,4-1,5=0,9. 2) Т.к. МО- средняя линия . Обозначим ВС=х, AD=y, тогда х+у=4,8. МО-ОN=0,6, МО+ОN=2,4. Тогда 2МО=3, МО=1,5. ON=2,4-1,5=0,9. 2) Т.к. МО- средняя линия 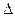 АВС, то МО= АВС, то МО=  ВС. Или ВС=2МО=3. 3) ON- средняя линия ВС. Или ВС=2МО=3. 3) ON- средняя линия 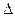 ACD, то ОN= ACD, то ОN=  AD. Или AD=2ОN=1,8. Ответ: 1,8; 3. AD. Или AD=2ОN=1,8. Ответ: 1,8; 3. |
12. Докажите, что отрезок, соединяющий середины диагоналей трапеции, параллелен основаниям и равен полуразности оснований.
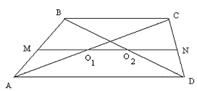 | Дано: ABCD- трапеция, АС и ВD диагонали, О1А=О1С. ВО2=О2D. Доказать: О1О2||ВC||AD, O1O2=  (AD-BC). Доказательство: 1) Проведем через середину отрезка АВ прямую параллельно ВС и AD. По определению MN является средней линией трапеции. Т.к. в (AD-BC). Доказательство: 1) Проведем через середину отрезка АВ прямую параллельно ВС и AD. По определению MN является средней линией трапеции. Т.к. в  АВС точки М и О1 являются серединами отрезков АВ и АС соответственно, то следовательно МО1 является средней линией АВС точки М и О1 являются серединами отрезков АВ и АС соответственно, то следовательно МО1 является средней линией  АВС, отсюда МО1= АВС, отсюда МО1=  ВС. Аналогично, видим, что NO2 является средней линией ВС. Аналогично, видим, что NO2 является средней линией  DBC и O2N= DBC и O2N=  ВС. Т.О. О1О2||DC||AD, MN= ВС. Т.О. О1О2||DC||AD, MN=  (ВС+AD), MN=MO1+O2N+O1O2. O1O2= MN-2BC- (ВС+AD), MN=MO1+O2N+O1O2. O1O2= MN-2BC-  ВС= ВС=  ВС+ ВС+  AD-BC= AD-BC=  (ВС-AD). (ВС-AD). |
13. Основания трапеции равны а и b. Две прямые, параллельные основаниям, делят одну из боковых сторон на три равные части. Найдите отрезки этих прямых, лежащие внутри трапеции.
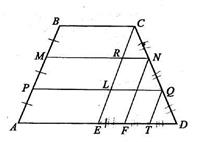 | Дано: ABCD-трапеция, ВС=а, AD=b, MN||PQ||BC||AD. MB=MP=PA. Найти: MN, PQ. Решение: 1) Так как на АВ отложены равные отрезки и через их концы проведены параллельные прямые MN и PQ, то по теореме Фалеса другая боковая сторона CD так же разделится на три равные части, T.e. CN=NQ=QD. 2) Проведем через точки С, N, Q прямые, параллельные стороне АВ. Т.е. СЕ||NF||QT||AB. Получим четырехугольник АВСЕ — параллелограмм, тогда ВС = АЕ = b, a ED = а—b. 3) Применяя теорему Фалеса (DQ=QN=NC; СЕ||NF||TQ), получим ЕF=FT=TD= 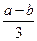 . Т.к. ET=LQ, то PQ= . Т.к. ET=LQ, то PQ= 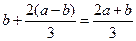 , а так как RN = EF, то MN = , а так как RN = EF, то MN = 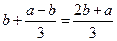 . Ответ: . Ответ: 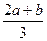 , , 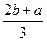 . . |
14. В трапеции АВCD боковая сторона АВ равна 5, а основание ВС равно 4. Какую из сторон трапеции, ВС и CD, пересекает биссектриса угла А этой трапеции?
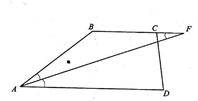 | Дано: ABCD-трапеция, AF- биссектриса  А. АВ=5, ВС=4. Найти AF А. АВ=5, ВС=4. Найти AF 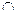 BC или AF BC или AF  CD -?. Решение: 1) CD -?. Решение: 1)  FAD= FAD=  AFB – как внутренние накрест лежащие углы при параллельных прямых AD и ВС и секущей AF. Тогда AFB – как внутренние накрест лежащие углы при параллельных прямых AD и ВС и секущей AF. Тогда  FAB= FAB=  AFB, а значит ∆АВС – равнобедренный, АВ=BF=5. По условию ВС=4, значит биссектриса угла А пересекает сторону CD. (Т.к. если бы точка F лежала бы на отрезке ВС, то мы получили бы противоречие с условием, т.е. мы получим равенство АВ=BF=5, но весь отрезок ВС=4, а т. F будет левее чем С). Ответ: CD. AFB, а значит ∆АВС – равнобедренный, АВ=BF=5. По условию ВС=4, значит биссектриса угла А пересекает сторону CD. (Т.к. если бы точка F лежала бы на отрезке ВС, то мы получили бы противоречие с условием, т.е. мы получим равенство АВ=BF=5, но весь отрезок ВС=4, а т. F будет левее чем С). Ответ: CD. |
15. В прямоугольной трапеции один из углов равен 1350, средняя линия равна 18 м, а основания относятся как 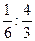 . Найдите меньшую боковую сторону трапеции.
. Найдите меньшую боковую сторону трапеции.
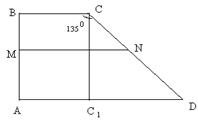 | Дано: ABCD- прямоуг. трапеция,  С=1350. MN=18, BC:AD= С=1350. MN=18, BC:AD= 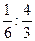 . Найти AB. Решение: . Найти AB. Решение: 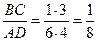 . Отсюда 8ВС=AD. Проведем высоту СС1. . Отсюда 8ВС=AD. Проведем высоту СС1.  С1CD=1350-900=450. Отсюда С1CD=1350-900=450. Отсюда  C1DC=450. Т.е. C1DC=450. Т.е. 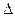 СС1D- равнобедренный и СС1=C1D. Пусть ВС=х, AD=y, тогда MN= СС1D- равнобедренный и СС1=C1D. Пусть ВС=х, AD=y, тогда MN=  (x+y), или х+у=36. AD=2BC. Или у=8х. Т.е. получили систему: (x+y), или х+у=36. AD=2BC. Или у=8х. Т.е. получили систему: 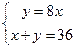 . Отсюда х=4, у=32. Тогда СС1=АВ=32-АС1=32-4=28. Ответ: 28. . Отсюда х=4, у=32. Тогда СС1=АВ=32-АС1=32-4=28. Ответ: 28. |
16. Найдите длину отрезка, параллельного основаниям трапеции (их длины a и b) и делящего трапецию на две равновеликие части.
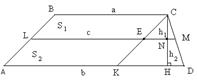 | Дано: ABCD- трапеция, ВС=а, АD=b, LM=c, LM||AD, SLBCM=SALMD. Найти c. Решение: 1) Пусть S1= SLBCM, S2= SALMD, S- площадь всей трапеции, h1, h2 – высоты верхней и нижней частей соответственно. Тогда составим систему: 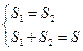 или или 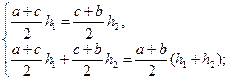 После подстановки первого уравнения во второе и преобразований получаем равенство: После подстановки первого уравнения во второе и преобразований получаем равенство: 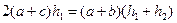 (*) 2) Проведем отрезок СК||АВ, ∆CKD~∆CEM по двум сторонам и углу между ними. (<C-общий, стороны содержащие этот угол пропорциональны). Отсюда (*) 2) Проведем отрезок СК||АВ, ∆CKD~∆CEM по двум сторонам и углу между ними. (<C-общий, стороны содержащие этот угол пропорциональны). Отсюда 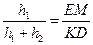 , , 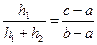 , но из равенства (*) имеем , но из равенства (*) имеем 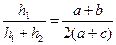 , поэтому , поэтому 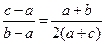 . Преобразуем последнее равенство . Преобразуем последнее равенство 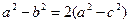 . . 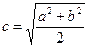 . . |
17. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 2: 1, считая от вершины острого угла. Найдите стороны параллелограмма, если его периметр равен 60 м.
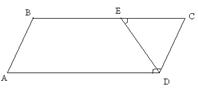 | Дано: ABCD- паралл-м, DE-биссектриса. ВЕ:ЕС=1:2. Р=60. Найти АВ и ВС. Решение: 1) Пусть АВ=х, ВС=у, тогда ВЕ+ЕС=у, ВЕ:ЕС=1:2, т.е. 2ВЕ=ЕС. Тогда 3ВЕ=у, ВЕ=у/3. 2) Т.к.  АDE= АDE=  CDE= CDE=  DEC (как внутренние накрест лежащие), то ЕС=СD=АВ=х. Тогда у-х=у/3. P=2(x+y)=60. x+y=30. т.е. получили систему: DEC (как внутренние накрест лежащие), то ЕС=СD=АВ=х. Тогда у-х=у/3. P=2(x+y)=60. x+y=30. т.е. получили систему: 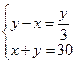 . Решая систему, получаем ответ: 12 и 18. Ответ: 12 и 18. . Решая систему, получаем ответ: 12 и 18. Ответ: 12 и 18. |
18. В параллелограмме ABCD AB = 5, ВС = 7. Биссектрисы внутренних углов, пересекаясь, образовали четырехугольник. Найдите отношение площади четырехугольника к площади параллелограмма.
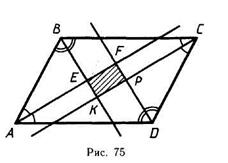 | Дано: ABCD- паралл-м, АВ=5, ВС=7, EFKP-четырехуг-к. Найти: SEFKP: SABCD. Решение: Пусть  BAD = α и BAD = α и  ABC=β. 1) Докажем, что четырехугольник EFPK – прямоугольник: α+ β= 1800. и ABC=β. 1) Докажем, что четырехугольник EFPK – прямоугольник: α+ β= 1800. и  BAE= BAE= 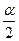 . .  ABE= ABE= 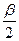 . Но . Но 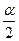 + + 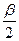 =900. Следовательно, =900. Следовательно,  АЕВ=900, а значит АЕВ=900, а значит  АЕК=900, и АЕК=900, и  КЕF=900, аналогично доказываются другие случаи с углами четырехугольника. 2) Пусть АВ=b, ВС=a. Тогда из треугольника ВКС BK = asin КЕF=900, аналогично доказываются другие случаи с углами четырехугольника. 2) Пусть АВ=b, ВС=a. Тогда из треугольника ВКС BK = asin 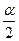 и из треугольника ABE BE = b sin и из треугольника ABE BE = b sin 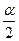 . Тогда ЕК = ВК – ВЕ =(a-b)sin . Тогда ЕК = ВК – ВЕ =(a-b)sin 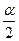 . Аналогично, EF=(a-b)cos . Аналогично, EF=(a-b)cos 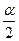 . Имеем: SEFKP = (a-b)2 sin . Имеем: SEFKP = (a-b)2 sin 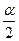 cos cos 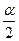 = =  (a-b)2 sinα. SABCD.=ab sinα. SEFKP: SABCD= (a-b)2 sinα. SABCD.=ab sinα. SEFKP: SABCD= 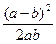 . Подставляя вместо а и b получим, что отношение SEFKP: SABCD=2:35. . Подставляя вместо а и b получим, что отношение SEFKP: SABCD=2:35. |
19. Биссектриса угла А параллелограмма ABCD пересекает сторону ВС в точке К и продолжение стороны CD в точке М; СМ = 1, ВК = 3. Найдите стороны параллелограмма.
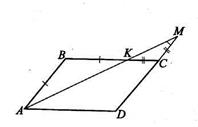 | Дано: ABCD-параллелограмм, АМ- биссектриса  А, К=BC А, К=BC 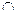 AM, M=AM AM, M=AM 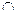 CD, CM=1, BK=3. Найти AB, BC. Решение: 1) CD, CM=1, BK=3. Найти AB, BC. Решение: 1)  BAK= BAK=  KAD, т.к. АК- биссектриса угла А, KAD, т.к. АК- биссектриса угла А,  ВКА= ВКА=  КАD как внутренние накрест лежащие при параллельных прямых AD и ВК и секущей АК. Откуда КАD как внутренние накрест лежащие при параллельных прямых AD и ВК и секущей АК. Откуда  ВАК= ВАК=  ВКА, значит, ∆АВК равнобедренный, АВ=ВК=3. ВКА, значит, ∆АВК равнобедренный, АВ=ВК=3.  ВАК= ВАК=  KMD как внутренние накрест лежащие при параллельных АВ и DM и секущей АМ. Из равенства этих углов следует, что ∆КМС равнобедренный и КС=СМ=1. Тогда ВС=1+3=4. Ответ: 3 и 4. KMD как внутренние накрест лежащие при параллельных АВ и DM и секущей АМ. Из равенства этих углов следует, что ∆КМС равнобедренный и КС=СМ=1. Тогда ВС=1+3=4. Ответ: 3 и 4. |
20. В равнобедренный прямоугольный треугольник вписан прямоугольник так, что две его вершины находятся на гипотенузе, а две другие – на катетах. Чему равны стороны прямоугольника, если известно, что они относятся как 5: 2, а гипотенуза треугольника равна 45 см?
 | Дано: ABC- прямоуг, равнобедр треугольник, LP:LM=5:2, AB=45, LM 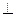 АВ. Найти LP, LM. Решение: 1) Пусть LM=х, LP=у, тогда AB=AM+NB+y=45. 2) Т.к. ∆AML прямоугольный, и АВ. Найти LP, LM. Решение: 1) Пусть LM=х, LP=у, тогда AB=AM+NB+y=45. 2) Т.к. ∆AML прямоугольный, и  А=450, то AM=LM=x=NB. Получили систему: А=450, то AM=LM=x=NB. Получили систему: 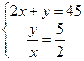 , решая систему, получаем ответ: 10 и 25. Ответ: 10 и 25. , решая систему, получаем ответ: 10 и 25. Ответ: 10 и 25. |
21. Докажите, что биссектрисы углов параллелограмма при пересечении образуют прямоугольник, диагонали которого параллельны сторонам параллелограмма и равны разности соседних сторон параллелограмма.
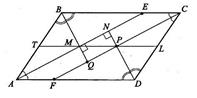 | Дано: ABCD-параллелограмм,. Доказать: 1) MNPQ —прямоугольник. 2)MP||AD. 3) MP=AD-AB. Решение: 1) В параллелограмме ABCD биссектрисы углов пересекаются в точках M,N,P и Q. Покажем, что MNPQ — прямоугольник.  AND = 1800 -( AND = 1800 -(  NAD+ NAD+  NDA)= NDA)=  ( ( A+ A+  D) = D) =  180° =90°. Аналогично оказывается, что остальные углы четырехугольника MNPQ — по 90°. 2) Покажем, что отрезок МР параллелен стороне AD. Обозначим точки пересечения прямых AM и СР со сторонами СВ и AD через Е и F. Заметим, что треугольники ABE и CFD равные равнобедренные с основаниями АЕ и CF соответственно. Биссектрисы углов при вершинах в этих треугольниках одновременно являются высотами, а значит, и медианами. Тогда четырехугольник MAFP — параллелограмм (АМ=FP, AM || FP), значит, отрезок МР||AD. Покажем, что МР =AD-AB. Продолжим отрезок МР до пересечения со сторонами АВ и CD точках T и L соответственно. По теореме Фалеса AT= ТВ, DL =LC, т.е. о трезки МТ и PL — медианы прямоугольных треугольников АМВ и CPD. По свойству медианы равнобедренного треугольника МТ= 180° =90°. Аналогично оказывается, что остальные углы четырехугольника MNPQ — по 90°. 2) Покажем, что отрезок МР параллелен стороне AD. Обозначим точки пересечения прямых AM и СР со сторонами СВ и AD через Е и F. Заметим, что треугольники ABE и CFD равные равнобедренные с основаниями АЕ и CF соответственно. Биссектрисы углов при вершинах в этих треугольниках одновременно являются высотами, а значит, и медианами. Тогда четырехугольник MAFP — параллелограмм (АМ=FP, AM || FP), значит, отрезок МР||AD. Покажем, что МР =AD-AB. Продолжим отрезок МР до пересечения со сторонами АВ и CD точках T и L соответственно. По теореме Фалеса AT= ТВ, DL =LC, т.е. о трезки МТ и PL — медианы прямоугольных треугольников АМВ и CPD. По свойству медианы равнобедренного треугольника МТ=  АВ, анало гично PL = АВ, анало гично PL =  CD, значит, МР =TL- CD, значит, МР =TL-  (АВ+CD)=AD-CD. (АВ+CD)=AD-CD. |
22. Из одной точки окружности проведены две взаимно перпендикулярные хорды, которые удалены от центра на 6 см и 10 см. Найдите их длины.
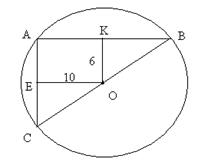 | Дано: Окр О, АВ 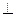 АС, ОК=6, ОЕ=10. Найти АВ, АС. Решение: 1) Пусть ВК=х, СЕ=у. Рассмотрим ∆ВКО: по т. Пифагора имеем АС, ОК=6, ОЕ=10. Найти АВ, АС. Решение: 1) Пусть ВК=х, СЕ=у. Рассмотрим ∆ВКО: по т. Пифагора имеем 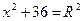 . Рассмотрим ∆СЕО: по т. Пифагора имеем . Рассмотрим ∆СЕО: по т. Пифагора имеем 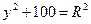 . Отсюда . Отсюда 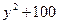 = = 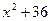 (1) 2) ∆ВКО~∆СЕО (по двум углам). (Т.к. (1) 2) ∆ВКО~∆СЕО (по двум углам). (Т.к.  В= В=  СОЕ, соответственные при параллельных прямых АС и ОК, АВ и ОЕ, СОЕ, соответственные при параллельных прямых АС и ОК, АВ и ОЕ,  ОКВ= ОКВ=  СЕО=900). Из подобия следует СЕО=900). Из подобия следует 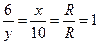 , т.е. 60=ху. (2). Получили систему: , т.е. 60=ху. (2). Получили систему: 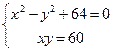 Решая систему, получаем решение: х=10. Отсюда АВ=20, АС=12. Ответ: 20 и 12. Решая систему, получаем решение: х=10. Отсюда АВ=20, АС=12. Ответ: 20 и 12. |
23. Биссектрисы углов В и С параллелограмма пересекаются в точке О на стороне АD. Найдите площадь параллелограмма, если ВС = 4 см, a  A = 60°.
A = 60°.
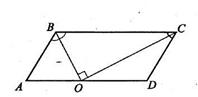 | Дано: АВСD - параллелограмм, ВС=4,  A = 60°, ВС, ОС - биссектрисы. Найти S. Решение: 1) Биссектрисы ВО и СО пересекаются в точке О, образуя прямой угол. Действительно, по свойству параллелограмма, сумма углов В и С равна 180°, а сумма половин этих углов — 90°. В прямоугольном ∆ ВОС: ВС = 4см, ВО =2см (катет, лежащий против угла 30°). Заметим, что площадь треугольника ВОС равна половине площади параллелограмма (для доказательства достаточно провести OF||CD). То гда площадь параллелограмма равна удвоенной площади треугольника: S = BC∙ABsin A = 60°, ВС, ОС - биссектрисы. Найти S. Решение: 1) Биссектрисы ВО и СО пересекаются в точке О, образуя прямой угол. Действительно, по свойству параллелограмма, сумма углов В и С равна 180°, а сумма половин этих углов — 90°. В прямоугольном ∆ ВОС: ВС = 4см, ВО =2см (катет, лежащий против угла 30°). Заметим, что площадь треугольника ВОС равна половине площади параллелограмма (для доказательства достаточно провести OF||CD). То гда площадь параллелограмма равна удвоенной площади треугольника: S = BC∙ABsin  СВО. Так как величина угла СВО равна 60°, то S=4∙2∙ СВО. Так как величина угла СВО равна 60°, то S=4∙2∙ 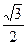 = = 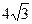 см2. Ответ: см2. Ответ: 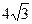 . . |
24. Найдите площадь трапеции с боковыми сторонами 13 и 20 и основаниями 6 и 27.
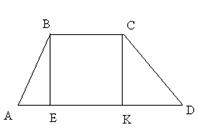 | Дано: АВСD - трапеция, АВ=13, CD=20, BC=6, AD=27. Найти S. Решение: 1) S=  h(BC+AD). Нужно найти высоту. Пусть АЕ=х, DK=у. Тогда AD=х+у+6=27. х+у=21 (1). 2) Рассмотрим ∆АВЕ: по т. Пифагора имеем АВ2-х2=h2. Рассмотрим ∆СDK: по т. Пифагора имеем CD2-y2=h2. Отсюда 132-x2=202-y2. Преобразуем уравнение, получим y2-x2=231. Или (у-х)(у+х)=231. Или 21(у-х)=231 (2). Получили систему: h(BC+AD). Нужно найти высоту. Пусть АЕ=х, DK=у. Тогда AD=х+у+6=27. х+у=21 (1). 2) Рассмотрим ∆АВЕ: по т. Пифагора имеем АВ2-х2=h2. Рассмотрим ∆СDK: по т. Пифагора имеем CD2-y2=h2. Отсюда 132-x2=202-y2. Преобразуем уравнение, получим y2-x2=231. Или (у-х)(у+х)=231. Или 21(у-х)=231 (2). Получили систему: 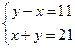 Решая систему, получаем решение: х=5, у=16. Отсюда h2=169-25=144. h=12. S= Решая систему, получаем решение: х=5, у=16. Отсюда h2=169-25=144. h=12. S=  12(6+27)=198. Ответ: 198. 12(6+27)=198. Ответ: 198. |
25. В параллелограмме площадью 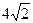 см2 отношение сторон равно отношению диагоналей; меньшая из диагоналей перпендикулярна одной из сторон параллелограмма. Найдите его стороны.
см2 отношение сторон равно отношению диагоналей; меньшая из диагоналей перпендикулярна одной из сторон параллелограмма. Найдите его стороны.
 | Дано: АВСD - параллелограмм,S= 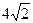 см2, АВ:AD = BD: АС=k. Найти AB, BC. Решение: По свойству параллелограмма 2 (АВ 2 + АD 2) =BD 2 +AC 2; 2(АВ 2 + k 2 АВ 2)=(BD 2 +k 2 BD 2); 2 АВ 2(1 +k 2) =BD2 (1 +k 2);2 АВ2=BD2; см2, АВ:AD = BD: АС=k. Найти AB, BC. Решение: По свойству параллелограмма 2 (АВ 2 + АD 2) =BD 2 +AC 2; 2(АВ 2 + k 2 АВ 2)=(BD 2 +k 2 BD 2); 2 АВ 2(1 +k 2) =BD2 (1 +k 2);2 АВ2=BD2; 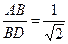 , , 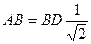 . S ABD = . S ABD = 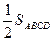 = = 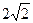 см2. Значит, см2. Значит, 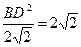 , BD= , BD= 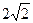 см, АВ=2см. По теореме Пифагора AD2=BD2+AB2=8+4=12, AD= см, АВ=2см. По теореме Пифагора AD2=BD2+AB2=8+4=12, AD= 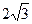 cм. cм. |
26. Сторона правильного вписанного в окружность треугольника равна 3. Найдите сторону квадрата, вписанного в эту окружность.
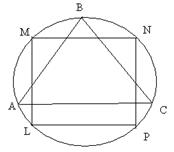 | Дано: Окружность О, ∆АВС, LMNP- квадрат вписанный в окружность. АВ=3. Найти LM. Решение: Из формулы, связывающей радиус и сторону треугольника: R= 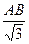 = = 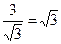 . Из формулы, связывающей радиус и сторону квадрата: R= . Из формулы, связывающей радиус и сторону квадрата: R= 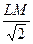 . . 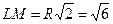 . Ответ: . Ответ: 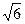 . . |
27. Найдите сторону и апофему правильного пятиугольника, вписанного в окружность радиуса R.
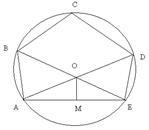 | Дано: (О,R), АВСDE – правильный 5-угольник. АВ=3. Найти АВ, ОМ. Решение: 1) сумма углов 5-угольника = 1800(n-2)= 1800*3=5400.  BAE=5400:5=1080. 2) АO- биссектриса BAE=5400:5=1080. 2) АO- биссектриса  А, тогда А, тогда  ОАЕ=1080:2=540. 3) ∆АОМ – прямоугольный, Тогда АМ=Rcos540. OM=Rsin540. AE=2Rcos540. Ответ: AE=2Rcos540, OM=Rsin540. ОАЕ=1080:2=540. 3) ∆АОМ – прямоугольный, Тогда АМ=Rcos540. OM=Rsin540. AE=2Rcos540. Ответ: AE=2Rcos540, OM=Rsin540. |
28. В прямоугольник со сторонами 3м и 4м вписан другой прямоугольник, стороны которого относятся как 1: 3. Найдите площадь этого прямоугольника.
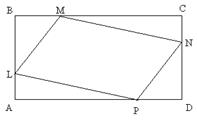 | Дано: АВСD и LMNP - прямоугольники. АВ=3. AD=4. LM:LP=1:3. Найти SLMNP. Решение: 1) Пусть PD=x, ND=y. 2) ∆LBM=∆PND по гипотенузе и острому углу. (LM=PN,  NPD= NPD=  BLM). 3) ∆LAP~∆PND по двум углам. ( BLM). 3) ∆LAP~∆PND по двум углам. ( NDP= NDP=  LAP=900, LAP=900,  ALP= ALP=  NPD – как углы со взаимно перпендикулярными сторонами). Из подобия треугольников следует: NPD – как углы со взаимно перпендикулярными сторонами). Из подобия треугольников следует: 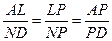 . AL=3-y, AP=4-x. Тогда . AL=3-y, AP=4-x. Тогда 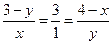 . Из пропорции составляем следующие системы: . Из пропорции составляем следующие системы: 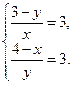 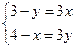 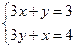 . Решим вторую систему. x=4-3y. Подставляем в 1-е уравнение: 3-у=3(4-3у). у= . Решим вторую систему. x=4-3y. Подставляем в 1-е уравнение: 3-у=3(4-3у). у= 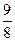 . х= . х= 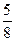 . 4) Т.к. ∆PND – прямоугольный, то PN= . 4) Т.к. ∆PND – прямоугольный, то PN= 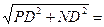 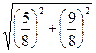 = = 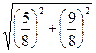 = = 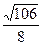 . 5) . 5) 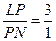 , LP=3PN= , LP=3PN= 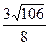 . 6) S=LP*NP= . 6) S=LP*NP= 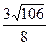 * * 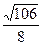 = = 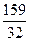 . Ответ: . Ответ: 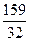 . . |
29. В параллелограмме угол между высотами равен α. Найдите высоты и площадь параллелограмма, если стороны его равны b и c.
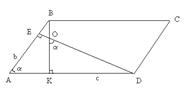 | Дано: АВСD – параллелограмм. АВ=b. BC=c,  KOD=α. Найти: SABCD, BK, DE. Решение: 1) KOD=α. Найти: SABCD, BK, DE. Решение: 1)  KDO=900-α. KDO=900-α.  ABK=900-α. ABK=900-α.  BAK=α. 2) ∆ABK – прямоугольный, Тогда BK=bsinα. 3) ∆AED – прямоугольный, Тогда ED=csinα. 4) S=bcsinα. Ответ: bsinα, csinα, S=bcsinα. BAK=α. 2) ∆ABK – прямоугольный, Тогда BK=bsinα. 3) ∆AED – прямоугольный, Тогда ED=csinα. 4) S=bcsinα. Ответ: bsinα, csinα, S=bcsinα. |
30. Внутри квадрата ABCD расположена точка М; МА = 7, МB = 3, МС = 5. Найдите сторону квадрата.
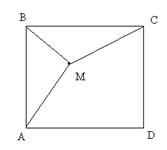 | Дано: ABCD квадрат. М 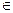 ABCD. МА = 7, МB = 3, МС = 5 Найти: АВ. Решение: Пусть ABCD. МА = 7, МB = 3, МС = 5 Найти: АВ. Решение: Пусть  АВМ=а, АВМ=а,  СВМ=β, АВ=х. Из ∆АВМ: 49=9+х2-6хcosa. (1) Из ∆СВМ: 25=9+х2-6хcosβ. (2) Из равенств (1) и (2): cosa= СВМ=β, АВ=х. Из ∆АВМ: 49=9+х2-6хcosa. (1) Из ∆СВМ: 25=9+х2-6хcosβ. (2) Из равенств (1) и (2): cosa= 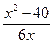 , cosβ= , cosβ= 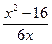 . Т.к. a+β=900, и cosa= cosβ, то . Т.к. a+β=900, и cosa= cosβ, то 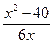 = = 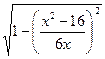 или или 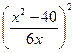 = = 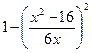 ( (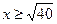 ). Преобразуем, получим x4-74x2+928=0. Отсюда х1= ). Преобразуем, получим x4-74x2+928=0. Отсюда х1= 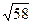 и х2=4 (посторонний корень, т.к.4< и х2=4 (посторонний корень, т.к.4< 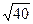 ). Ответ: ). Ответ: 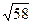 |
31. Периметр ромба равен 2 р, сумма диагоналей его с. Найдите площадь ромба.
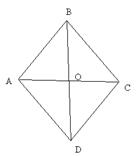 | Дано: АВСD – ромб. р=2р. АС+BD=с. Найти: SABCD. Решение: 1) р=4АВ=2р. АВ= 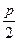 . d1+d2=c. AO= . d1+d2=c. AO= 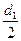 , BO= , BO= 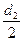 . 2) AB2= . 2) AB2= 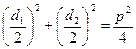 , , 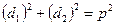 . Получили систему: . Получили систему: 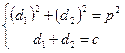 . Возведем 2-е уравнение в квадрат: . Возведем 2-е уравнение в квадрат: 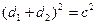 . . 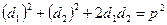 Из 1-го: Из 1-го: 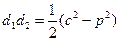 . 3) S= . 3) S= 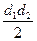 = = 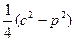 . Ответ: . Ответ: 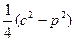 . . |
32. Высота ромба равна 6 см. Его острый угол равен 300. Найдите диагонали ромба. (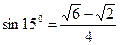 ).
).
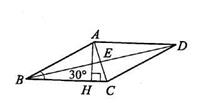 | Дано: АВСD–ромб. АН 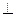 ВС. ВС.  В=300, Е=BD В=300, Е=BD  AC. Найти:BD, AC. Решение: Из прямоугольного треугольника АВН имеем: AC. Найти:BD, AC. Решение: Из прямоугольного треугольника АВН имеем: 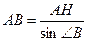 =12cм. По свойству диагонали ромба =12cм. По свойству диагонали ромба  ABD= ABD=   ABC=150. Далее из прямоугольного треугольника АВЕ имеем: АЕ = АВ∙sin150= ABC=150. Далее из прямоугольного треугольника АВЕ имеем: АЕ = АВ∙sin150= 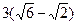 . Заметим, что cos150= . Заметим, что cos150= 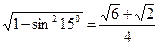 . Тогда ВЕ=АВ∙cos150= . Тогда ВЕ=АВ∙cos150= 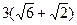 . Далее находим: АС=2АЕ= . Далее находим: АС=2АЕ= 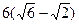 , BD=2BE= , BD=2BE= 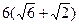 . . |
33. В равнобедренной трапеции, описанной около круга, острый угол при основании равен α. Найдите отношение площади круга к площади трапеции.
 | Дано: АВСD – трапеция,  А=α. Найти: А=α. Найти: 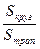 . Решение: 1) . Решение: 1) 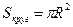 , , 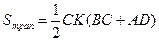 . Пусть CD=x, CK=h. 2) ME - диаметр, МЕ=2R=h. 3) ∆AED – прямоугольный, . Пусть CD=x, CK=h. 2) ME - диаметр, МЕ=2R=h. 3) ∆AED – прямоугольный, 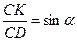 . Отсюда h=xsinα. Итак, получили: h=xsinα, 2R=h. Т.е. 2R=xsinα. R= . Отсюда h=xsinα. Итак, получили: h=xsinα, 2R=h. Т.е. 2R=xsinα. R= 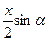 . 4) . 4) 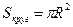 = = 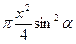 = = 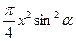 . 5) По свойству сторон описанного 4-угольника, следует: BC+AD=AB+CD. Или BC+AD=2x. 6) . 5) По свойству сторон описанного 4-угольника, следует: BC+AD=AB+CD. Или BC+AD=2x. 6) 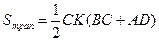 = = 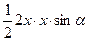 = = 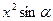 . . 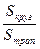 = = 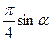 . . |
34. К окружности радиуса R проведены 4 касательные, образующие ромб, большая диагональ которого равна 4 R. Найдите площадь каждой из фигур, ограниченных двумя касательными, проведенными из общей точки, и дугой окружности, лежащей между соседними точками касания.
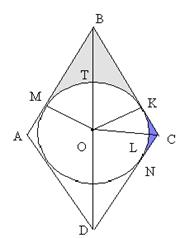 | Дано: АВСD – ромб, BD=4R. OK=R. Найти: SMBKT, SNCKL. Решение: 1)Пусть S1= SMBKT, S2= SNCKL. 2) BD=4R, BO=2R, OM=R. (ОМ- лежит против угла в 300). MB= 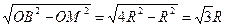 . 3) SMBKO=SMBO+SOBK=2SMBO= . 3) SMBKO=SMBO+SOBK=2SMBO= 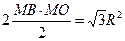 . 4) Т.к. . 4) Т.к.  МОВ=600, то МОВ=600, то  МОК=1200, то площадь сектора MOКT равна МОК=1200, то площадь сектора MOКT равна 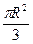 . Тогда S1= . Тогда S1= 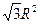 - - 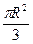 = = 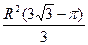 . 5) Аналогично рассуждая, получим, что S2= . 5) Аналогично рассуждая, получим, что S2= 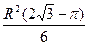 . . |
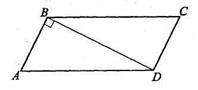
35. Вромбе ABCD из вершины D опущен перпендикуляр DK на сторону BC. Найдите длину стороны ромба, если AC = 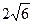 , АК =
, АК = 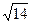 .
.
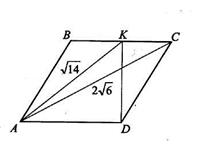 | Дано: АВСD – ромб, DK 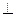 BC. AC= BC. AC= 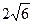 , АК = , АК = 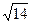 . Найти: AB. Решение: 1)Пусть АВ=х, . Найти: AB. Решение: 1)Пусть АВ=х,  С=α. Из ∆ CDK имеем: DK = xsinα; из ∆ AKD: 14= х 2+(xsinα)2, откуда sin2α = С=α. Из ∆ CDK имеем: DK = xsinα; из ∆ AKD: 14= х 2+(xsinα)2, откуда sin2α = 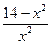 (1). В ∆ ADC (1). В ∆ ADC  D=π-α, тогда по теореме косинусов 24= х 2 +х 2 – 2 x cos(p-α), откуда 12 = х 2+x2cosα; cosα= D=π-α, тогда по теореме косинусов 24= х 2 +х 2 – 2 x cos(p-α), откуда 12 = х 2+x2cosα; cosα= 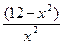 ; cos2α= ; cos2α= 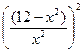 (2). Сложив равенства (1) и (2), получим: 1= (2). Сложив равенства (1) и (2), получим: 1= 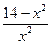 + + 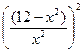 . Решая это уравнение, получим х = . Решая это уравнение, получим х = 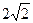 . . |
36. На сторонах AD и DC ромба ABCD построены правильные треугольники AKD и DMC так, что точка К лежит по ту же сторону от AD, что и прямая ВС, а точка М – по другую сторону от DC, чем АВ. Докажите, что точки В, К и М лежат на одной прямой.
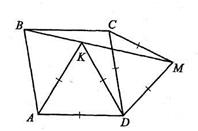 | Дано: АВСD – ромб. Доказать: В, К, М – лежат на одной прямой. Док-во: Пусть  ВАD=α. Найдем величину угла ВКМ. ВАD=α. Найдем величину угла ВКМ.  ВАК=α-600, ВАК=α-600,  АВК= АВК=  ВКА=1200- ВКА=1200- 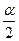 , ,  MDK=1800-α, MDK=1800-α,  MKD = MKD =  DMK = DMK = 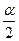 . .  BKM= BKM=  BKA+ BKA+  AKD+ AKD+  MKD=1200- MKD=1200- 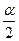 +600+ +600+ 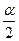 =1800. Значит, угол ВКМ – развернутый, т.е. точки В, К, М – лежат на одной прямой. =1800. Значит, угол ВКМ – развернутый, т.е. точки В, К, М – лежат на одной прямой. |
37. Точки M, P, Q и R – середины сторон ромба ABCD. Докажите, что четырехугольник MPQR – прямоугольник.
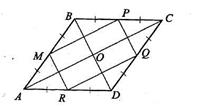 | Дано: АВСD – ромб. Доказать: MPQR – прямоугольник. Док-во: Отрезки МР и QR — средние линии треугольников ABC и ADC соответственно, по свойству средней линии треугольника они равны половине стороны АС ипараллельны ей. Тогда четырехугольник MPQR — параллелограмм. Аналогично MR||PQ.  PMR= PMR=  BOC как углы с соответственно параллельными сторонами. По свойству диагоналей ромба BOC как углы с соответственно параллельными сторонами. По свойству диагоналей ромба  BOC =90°, значит, в параллелограмме MPQR BOC =90°, значит, в параллелограмме MPQR  М =900, т.е. этот параллелограмм — прямоугольник. М =900, т.е. этот параллелограмм — прямоугольник. |
38. В ромбе ABCD один из углов равен 60°. Докажите, что если угол NBМ треугольника BMN равен 60°, то и остальные его углы тоже по 60°.
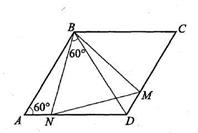 | Дано: АВСD – ромб.  А=600. Доказать:. Док-во: Пусть А=600. Доказать:. Док-во: Пусть  NBM= 60°, покажем, что остальные углы треугольника BMN по 60°. Заметим, что NBM= 60°, покажем, что остальные углы треугольника BMN по 60°. Заметим, что  ABD= 60°. Тогда ABD= 60°. Тогда  АВN= АВN=  DBM,в треугольниках ABN и DBM равны стороны АВ и BD, углы ABN и DBM, BAN и BDM. Следовательно, эти треугольники равны, и равны их соответственные стороны: BN=BM. В равнобедренном треугольнике NBM угол при вершине 60°, значит, такой треугольник — правильный. DBM,в треугольниках ABN и DBM равны стороны АВ и BD, углы ABN и DBM, BAN и BDM. Следовательно, эти треугольники равны, и равны их соответственные стороны: BN=BM. В равнобедренном треугольнике NBM угол при вершине 60°, значит, такой треугольник — правильный. |
39. Высота ромба, проведенная из вершины его тупого угла, делит сторону ромба в отношении 1: 2, считая от вершины его острого угла. Какую часть площади ромба составляет площадь вписанного в него круга?
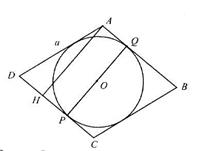 | Дано: АВСD – ромб. АН-высота, DH:CH=1:2, O- центр вписанной окружности. Найти: 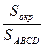 . Решение: Пусть сторона ромба равна а, тогда DH= . Решение: Пусть сторона ромба равна а, тогда DH= 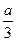 , по теореме Пифагора АН= , по теореме Пифагора АН= 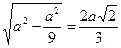 . Проведем PQ . Проведем PQ 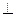 DC через точку О. Так как PQ=AH, то радиус окружности равен DC через точку О. Так как PQ=AH, то радиус окружности равен 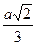 ; Sокр=πR2, ; Sокр=πR2, 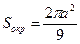 ; ; 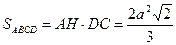 . . 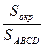 = = 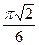 . . |
40. На сторонах АВ и CD прямоугольника ABCD взяты точки K и М так, что четырехугольник AKCM – ромб. Диагональ АС составляет со стороной АВ угол 300. Найдите сторону ромба, если наибольшая сторона прямоугольника равна 3.
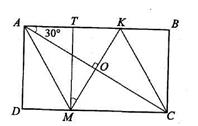 | Дано: АВСD – прямоугольник. AKCM – ромб.  САВ=300, АВ=3. Найти: АМ. Решение: По условию САВ=300, АВ=3. Найти: АМ. Решение: По условию  ВАС= 30°, АВ = 3. Тогда из прямоугольного ∆ ABC находим: ВС=ABtg30°= ВАС= 30°, АВ = 3. Тогда из прямоугольного ∆ ABC находим: ВС=ABtg30°= 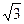 , АС= , АС= 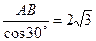 . Проведем МТ . Проведем МТ  АВ. АВ.  KMT = KMT =  CAK как углы с соответственно перпендикулярными сторонами. Тогда из прямоугольного ∆ КМТ: КМ=ТМ: cos30° = CAK как углы с соответственно перпендикулярными сторонами. Тогда из прямоугольного ∆ КМТ: КМ=ТМ: cos30° = 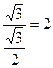 . Сторону ромба найдем из треугольника СОМ ( . Сторону ромба найдем из треугольника СОМ ( СОМ между диагоналями ро СОМ между диагоналями ро
Подборка статей по вашей теме:
|
 2015-08-21
2015-08-21 2284
2284