Определение

Пусть 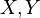— две случайные величины, определённые на одном и том же вероятностном пространстве. Тогда их ковариация определяется следующим образом:

,

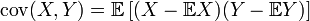где 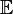— оператор математического ожидания.

Предполагается, что все математические ожидания 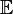в правой части данного выражения определены.

Замечания

Если 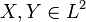, то есть имеют конечный второй момент, то ковариация определена и конечна.

В гильбертовом пространстве несмещённых случайных величин с конечным вторым моментом 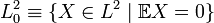ковариация имеет вид 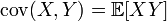и играет роль скалярного произведения.