Главная часть

Содержание

Введение…………………………………………………………………………...3

Главная часть……………………………………………………………………4

Заключение……………………………………………………………………….10

Список литературы………………………………………………………………11

Введение

Мажоритарный элемент позволяет обеспечить режим одновременного штатного функционирования основного и резервных элементов РЭУ и исключает применение специальных коммутационных узлов, устраняющих взаимное влияние основного и резервных элементов друг на друга. При этом отказ основного или резервного элементов не влияет на работу оставшихся исправных элементов. В настоящее время нашло весьма широкое применение структурное резервирование с

мажоритарным элементом, оно используется для повышения надежности цифровых электронных устройств и цифровых систем.

Главная часть

Мажоритарный элемент — это логическое устройство с нечетным числом входов

m=2k+1 (где k = 1, 2,3.) и одним выходом. Чаще всего используются элементы

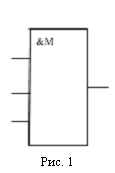
с m = 3, реже с m = 5 и совсем редко с m = 7. Условное

обозначение мажоритарных элементов показано на рис. 1.

Мажоритарный элемент может быть выполнен в виде отдельной микросхемы или

собран из нескольких логических микросхем. В дальнейшем для краткости будем

называть резервирование с применением мажоритарного элемента просто

мажоритарным резервированием.

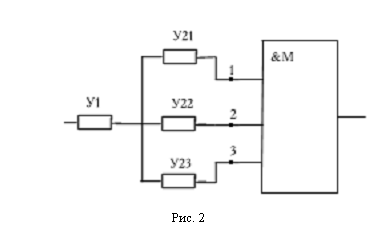
Принцип мажоритарного резервирования поясним на примере с помощью рис. 2,

отображающего часть некоторой цифровой схемы.

С выхода цифрового устройства У1 цифровые сигналы в виде последовательности

символов «0» и «1» поступают на входы трех работающих одновременно одинаковых

равно надежных устройств У21, У22, У23, образующих резервированный узел.

Цифровые сигналы с выхода каждого из устройств У21, У22, У23 поступают на

соответствующий вход мажоритарного элемента (в данном случае трехвходового).

Если каждое из устройств У21, У22, У23 исправно, то в данный момент времени

на их выходах будет один и тот же двоичный символ (0 или 1), а значит и на

входах мажоритарного элемента. Тогда и на выходе мажоритарного элемента будет

такой же двоичный сигнал. Если какое-либо из устройств У21, У22, У23

отказало, то только на двух входах мажоритарного элемента в данный момент

времени двоичные символы будут одинаковые. На выходе же мажоритарного

элемента будет двоичный символ, совпадающий с символом на выходе двух

исправных устройств. То есть мажоритарный элемент выполняет логическую

операцию принятия решения «по большинству» (операция «голосования»). Теперь

становится понятным, почему количество входов у мажоритарного элемента должно

быть нечетным и больше единицы.

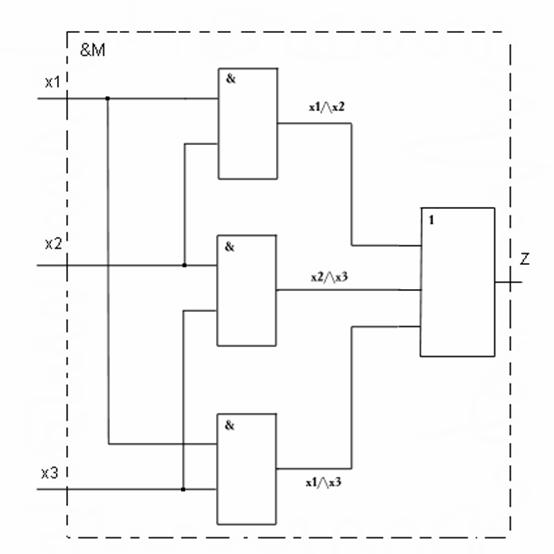
На рис. 3 изображена структурная схема трехвходового мажоритарного элемента, из

которой становится понятной логика его работы, отвечающая логической функции

Z=(x1 /\ x2) \/ (x2/|x3)\/(x1/|x3).

Найдем зависимость вероятности безотказной работы узла с мажоритарным

резервированием P_рм(t) от вероятности безотказной работы

резервируемого и резервных элементов P(t). Начнем с частного случая,

отвечающего трехвходовому мажоритарному элементу. Предполагаем при этом, что

сам мажоритарный элемент абсолютно надежен.

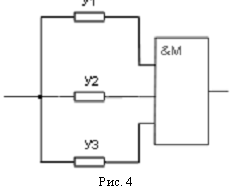
Узел на рис. 4 будет работоспособным, если он находиться в следующих двух

состояниях.

Состояние 1. Работоспособны и У1, и У2, и У3. Вероятность нахождения узла

в таком состоянии:

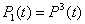
Состояние 2. Работоспосбны любые два устройства из У1, У2, У3.

Вероятность такого состояния:

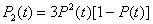
Во всех прочих состояниях узел на рис. 4 будет в отказе.

Таким образом, вероятность безотказной работы узла определяется суммой:

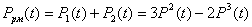
Рассуждая аналогично, можно найти P_рм(t) при m=5,

m=7 и т.д. В общем случае зависимость P_рм (t) от P(t)

имеет вид

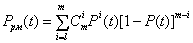
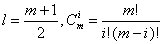
где — число сочетаний из m по i.

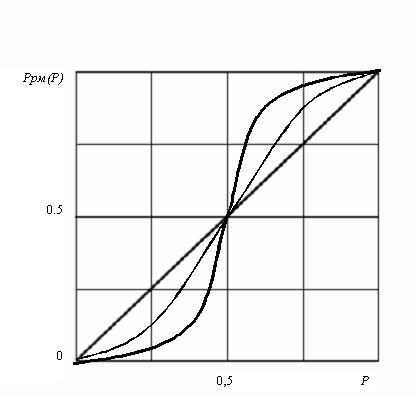
На рисунке 5 показано семейство функций P_рм (t) при

t=const и различных m. Анализ поведения этих функций позволяет

сделать важный вывод, что мажоритарное резервирование дает положительный

эффект, пока P>0.5, в противном случае надежность устройства

понижается.

Устройства с мажоритарным резервированием, как и с любым другим, являются

стареющими с точки зрения надежности, то есть интенсивность отказов таких

устройств со временем растет.

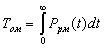Среднюю наработку T_ом

узла с мажоритарным резервированием в общем случае с помощью формулы определить

затруднительно.

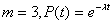
Найдем T_ом для часто встречающегося случая при

Воспользуемся при нахождении P_рм(t) общей формулой или ее частным случаем:

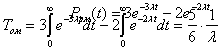
Тогда

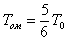
или

Из этого следует, что T_ом < T₀ и на первый взгляд это неожиданно.

Уменьшает ли резервирование среднюю наработку? Ответ следует искать в

"особенности старения" узла с мажоритарным резервированием.

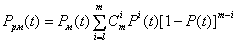
На практике нельзя считать мажоритарный элемент абсолютно надежным. Он обладает

известной вероятностью безотказной работы P_м(t). При расчете

надежности это обстоятельство учитывается включением мажоритарного элемента

последовательно за резервируемым узлом. Тогда общая формула с учетом надежности

самого мажоритарного элемента трансформируется в иную:

Сопоставим по надежности мажоритарное резервирование с обычным постоянным. При

сопоставлении в качестве показателей надежности используем вероятности отказа

узлов с резервированием Q_рм(t) и Q_р(t).

Сопоставление осуществим для случая, когда

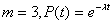
Найдем вероятность безотказной работы узлов:

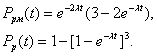
Принимая во внимание, что при lt << 1

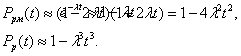
получаем

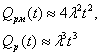
От сюда следует, что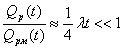

и

то есть Q_рм(t) >> Q_р(t).