Завдання №1
У таблиці 1 наведені результати спостережень за кількістю студентів, що заходять до 18 корпусу впродовж однієї хвилини.
Таблиця 1
| Кількість студентів | Розподіл (частка вказаної кількості студентів) |
| < 4 | Відсутні |
| 0.21 | |
| 0.12 | |
| 0.12 | |
| 0.15 | |
| 0.20 | |
| 0.20 | |
| > 9 | Відсутні |
Генератором випадкових чисел були згенеровані наступні числа:
0.85; 0.50; 0.39; 0.38; 0.64.
1) Побудувати кумулятивний розподіл та промоделювати 5 хв., використовуючи ці випадкові числа та дані, що наведені в таблиці.
2) Визначити кількість студентів, що надходили до корпусу щохвилини, а також середню кількість студентів за 5 промодельованих хвилин.
Розв’язання
Побудуємо кумулятивний розподіл, виходячи з таблиці 1:
| Кількість студентів | Розподіл (частка вказаної кількості студентів) | Кумулятивний розподіл |
| < 4 | Відсутні | |
| 0.21 | 0.21 | |
| 0.12 | 0.33 | |
| 0.12 | 0.45 | |
| 0.15 | 0.60 | |
| 0.20 | 0.80 | |
| 0.20 | 1.00 | |
| > 9 | Відсутні |
Використовуючи задані випадкові числа та дані кумулятивного розподілу, знайдемо послідовні кількості студентів.
Принцип знаходження кількості студентів, що увійшли в корпус за 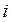 -ту хвилину, в залежності від випадкового числа
-ту хвилину, в залежності від випадкового числа 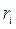 можна проілюструвати за допомогою графіка, що представлений на рисунку 1.
можна проілюструвати за допомогою графіка, що представлений на рисунку 1.
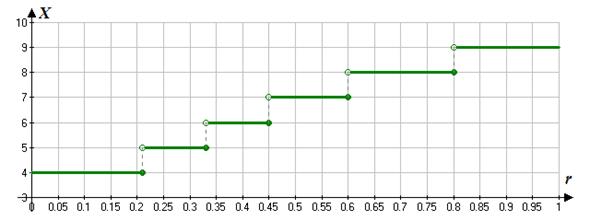
Рисунок 1 – Графік залежності кількості студентів за 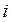 -ту хвилину від випадкового числа
-ту хвилину від випадкового числа 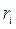 , побудований за кумулятивним розподілом
, побудований за кумулятивним розподілом
Отже, знайдені кількості студентів:
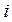 -та хвилина -та хвилина
| Випадкове число 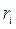
| Кількість студентів в 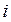 -ту хвилину -ту хвилину 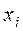
|
| 0.85 | ||
| 0.50 | ||
| 0.39 | ||
| 0.38 | ||
| 0.64 |
Знайдемо середню кількість студентів за ці 5 хвилин: 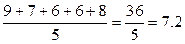 .
.
| Відповідь Кількість студентів (похвилинно): 9, 7, 6, 6, 8. Середня кількість: 7.2. |
 2015-08-21
2015-08-21 262
262







